Flat-form clustering

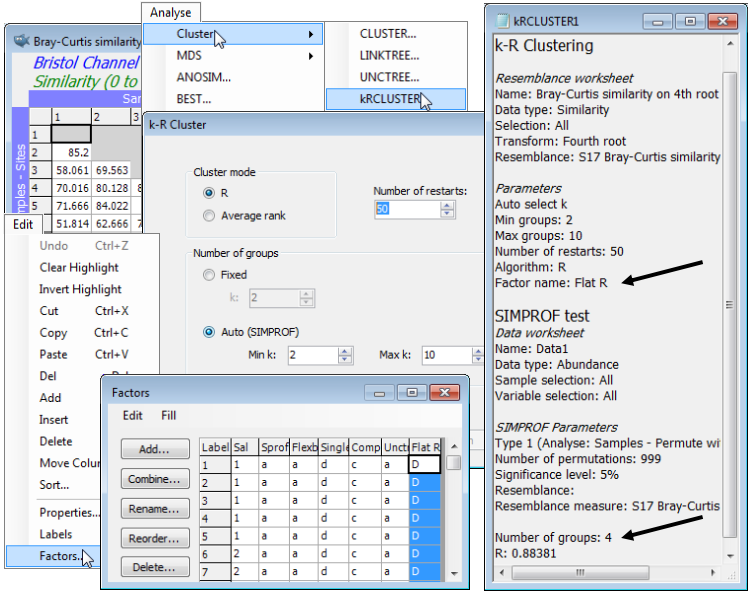
Another new introduction in PRIMER 7 is a form of non-hierarchical (flat) clustering, the analogue of the k-means method in traditional cluster analysis. The latter is a widely-used technique based on Euclidean distances in the variable space of the original data matrix, seeking to form an optimal division of samples into a specified number of groups (k), minimising the within-group sums of squares about the k group ‘centres’ (termed centroids) in that high-dimensional variable space. However, in that form, it is quite inappropriate for typical species matrices, for which Euclidean distances or their squares (whether on normalised variables or not) are a poor measure of dissimil¬arity among samples, as discussed in Section 5 and in more detail in Chapters 2 and 16 of CiMC. What is required here, to be consistent with the rest of the PRIMER package (and the hierarchical methods previously described) is a technique which applies to any dissimilarity coefficient, and in particular, those suitable for species data (e.g. Bray-Curtis). By analogy with k-means, the concept of k-R clustering is introduced towards the end of Chapter 3 of CiMC, in which the k groups are chosen to maximise the global ANOSIM R statistic (as it would be calculated for an ANOSIM test of the k groups involved). Again, the use of R here has nothing to do with hypothesis testing; it is its usefulness as a completely general measure of separation of defined groups of samples, based only on the ranks of the dissimilarity matrix – the same numbers, however that dissimilarity is defined – which is being exploited. Above, we used the idea of maximising R for a division of the samples into two groups; here the kRCLUSTER routine simply generalises that to maximising R calculated over k groups. It again involves a demanding iterative search, with user choice of the number of random restarts (again the current default is 10 but try more if the process runs quickly).

A perceived drawback of the k-means approach is that k must be specified in advance. There may be situations in which a pre-fixed number of groups is required but, more likely, it would be useful to determine the ‘best k’ from a range of values, in some well-defined sense. SIMPROF tests can be exploited here also, to provide a possible stopping rule. The k-R Cluster dialog asks for min and max k values to try, and starting with (say) the default min k of 2, finds the optimal division into two groups and tests those groups, with SIMPROF, for evidence of within-group structure. So far, these groups and the tests will be exactly those of the unconstrained binary divisive (UNCTREE) routine, above. But these groups are not then further subdivided – this is not a hierarchical process. If at least one SIMPROF test is significant then these groups are thrown away, and the procedure starts again with the full set of samples and attempts to find an optimal k=3 group solution. These groups are again tested with SIMPROF, and if any of the three tests is significant, a k=4 solution is sought on the full set of samples, etc. The procedure stops either when the specified max k (default 10) has been explored or when all SIMPROF tests for the current k are not significant (i.e. there is no statistical evidence of structure at a finer-scale than this k-group partition). kRCLUSTER will request a factor name to define that grouping; note that it is a single factor holding only the solution for the (optimum or maximum) k-value at which the procedure terminates. A tree diagram cannot, of course, be plotted, since there is no hierarchy. In fact, the reason for exploring flat clustering of this type is to avoid the inflexibility, in hierarchical methods, of samples being unable to ‘change their allegiance’ – once in a specific group, a sample remains in a subset or superset of that group.

A final choice on the k-R Cluster dialog is between (Cluster mode•R), which is precisely the rank- based algorithm described above, and (Cluster mode•Average rank), which is a subtle variation bearing some analogy with group average linkage (an idea met in agglomerative clustering but here still used to produce a flat clustering). The last page of Chapter 3 of CiMC explains this variation, which (though not using R as such) is still a function only of the ranks of the original resemblance matrix. In practice, the two flat-clustering modes should produce rather similar solutions.

Again on the Bristol Channel zooplankton data, whose workspace should still be open, with the active sheet as the Bray-Curtis similarity matrix based on fourth-root transformed densities, take Analyse>Cluster>kRCLUSTER>(Cluster mode•R) & ((Number of groups•Auto (SIMPROF))> (Min k: 2) & (Max k: 10)) & (Number of restarts: 50), and with defaults taken on the SIMPROF options dialog, and specifying factor for the optimal grouping of Flat R. The results are inevitably rather minimal in this case: the results window gives the optimal number of groups again as k=4 (with R=0.884), and Edit>Factors will show the Flat R grouping. You may like to run the routine again with (Cluster mode•Average rank), which results in the same k=4 groups here, though the factor sheet shows that the order of assignment of letters A, B, C, D to the 4 groups may differ. This is an inevitable result of the random search procedure, even when the same options are taken.

In fact, much the best way of comparing the results of the differing clustering methods of this section is seen for these data in Fig. 3.10 of CiMC, namely on three copies of the same non-metric MDS ordination of the 57 samples. See Section 8 for running MDS ordinations, so this example will not be pursued further here (but you might like to return to these data after tackling Section 8 and reproduce a larger version of Fig. 3.10, covering all the variations of clustering methods you have generated in this section, so Save Workspace As>File name: Bristol Channel ws). In Fig. 3.10, the differing SIMPROF group factors SprofGps, Unctree and Flat R – for the hierarchical agglomerative (group average), divisive and flat clusters – are plotted as symbols, and relettered consistently, since essentially the same four main groups result from these very different clustering techniques. The minor differences between methods are clear: they just concern allocation of a few sites, which tend to be intermediate between the main groups – the treatment of sites 9, 23 and 24 is all that distinguishes them.

This is exactly what one might wish for in drawing solidly-based inference of clustering structure – a stability to the choice of method. It is relevant here that the same transformation and (especially) similarity matrix was used for all methods. Major differences in groupings would be expected to arise from using different pretreatments or dissimilarity definitions, e.g. comparing SIMPROF groups from agglomerative clusters, using Bray-Curtis on fourth-root transformed densities, with SIMPROF groups from a method closer to traditional k-means clustering (normalised species data, with resemblances calculated using Euclidean distance, and analysed by the Average rank cluster mode of the above k-R clustering). This has rather little to do with choice of clustering method but everything to do with what is understood by similarity of samples in the high-dimensional species space. This is a recurring theme in CiMC: the major differences between ordination methods such as PCA (Section 12) and nMDS (Section 8) usually has much less to do with the different way the methods try to view high-d data in low-d space, but much more to do with how those methods choose to define ‘distances’ in that high-d space at the outset (PCA by Euclidean distance, nMDS often by a species-based community measure from the Bray-Curtis family).