Skip to main content

1.21 Components of variation

For any given ANOVA design, PERMANOVA identifies a component of variation for each term in the model, denoted as ‘S(*)’ for the fixed terms and ‘V(*)’ for the random terms. This notation is used because, in the analogous univariate case, components of variation for a fixed factor are sums of squared fixed effects (divided by appropriate degrees of freedom), while components of variation due to random factors are actual measures of variability or variance components. This is appropriate, because the hypotheses are also different in these two cases. For fixed effects, the hypothesis only concerns the effects of those levels that were included in the experiment, whereas for the random factor, the hypothesis is about the variability among a population of levels, of which the levels in the experiment are a random representative sample. Note that any interaction involving a random factor will also be random. The residual component is also denoted by ‘V(Res)’ because it too is a measure of variability. Thus, for example, in the two-way mixed model design for the Tasmanian meiofauna, the total variation is partitioned according to four sources, as follows:

  • S(Tr): sum of squared treatment effects (divided by degrees of freedom);

  • V(Bl): variation due to blocks;

  • V(TrxBl): variation in treatment effects among blocks; and

  • V(Res): residual variation.

Note that if one is using PERMANOVA to analyse a single variable with Euclidean distance, then the components of variation are indeed true variance components (for random factors) and true sums of squared fixed effects divided by degrees of freedom (for fixed factors). Here and in PERMANOVA, they are simply called components of variation, however, in order to cover the more general cases, including the analysis of many variables on the basis of non-Euclidean resemblance measures.

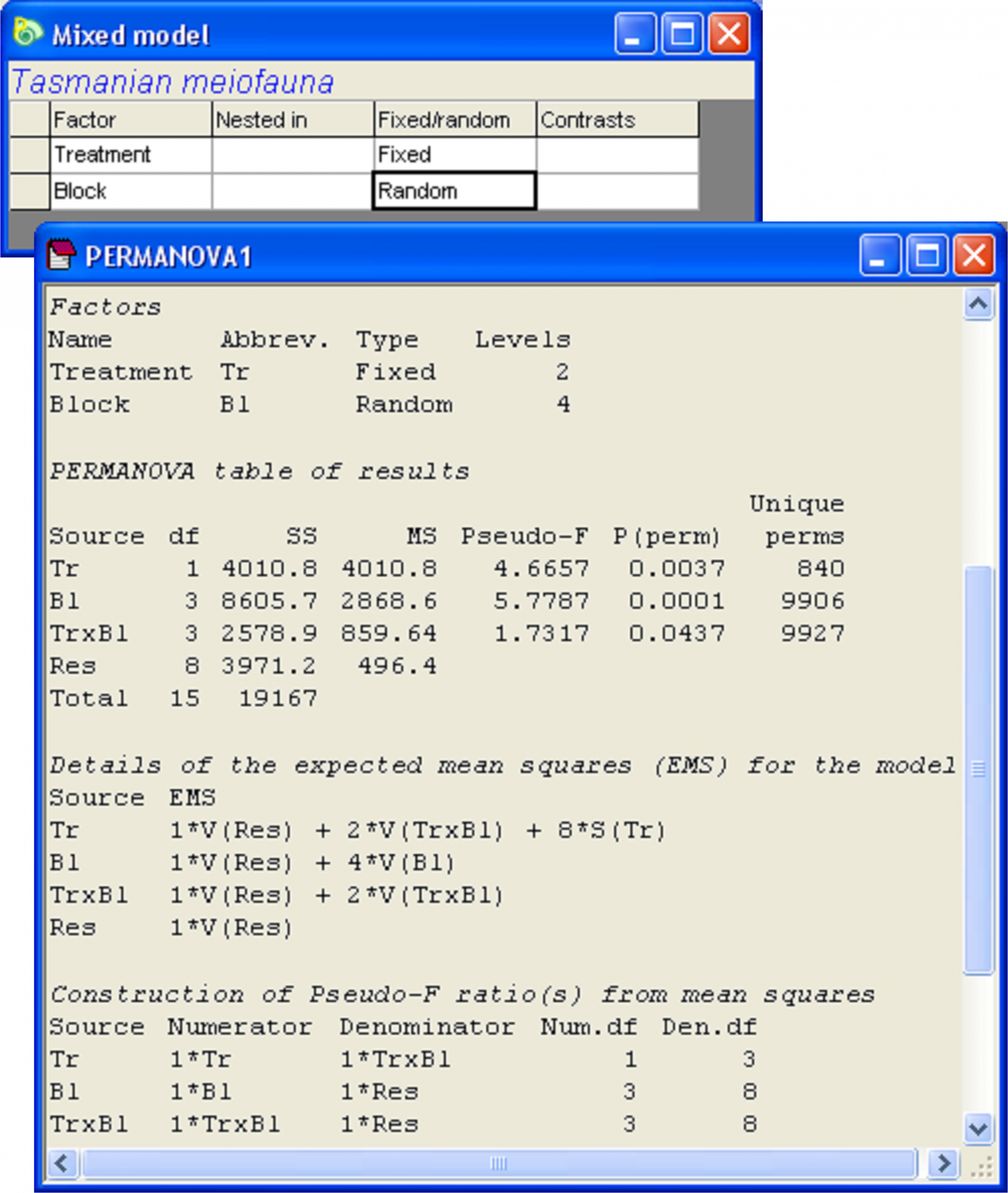Fig1.23.png Fig. 1.23. Design file and PERMANOVA results for the Tasmanian meiofauna, including details of the expected mean squares and construction of F ratios for each term in the mixed model

Back to top