Skip to main content

5.3 Mechanics of CAP

Details of CAP and how it is related to other methods are provided by Anderson & Robinson (2003) and Anderson & Willis (2003) . In brief, a classical canonical analysis is simply done on a subset of the PCO axes. Here, we provide a thumbnail sketch to outline the main features of the analysis. The important issues to keep in mind are the conceptual ones, but a little matrix algebra is included here for completeness. Let D be an N × N matrix of dissimilarities (or distances) among samples99. Let X be an N × q matrix that contains either codes for groups (for discriminant analysis) or one or more quantitative variables of interest (for canonical correlation analysis). Conceptually, we can consider X to contain the hypothesis of interest. When using CAP for discriminant analysis in the PERMANOVA+ add-on package for PRIMER, groups are identified by a factor associated with the resemblance matrix. The CAP routine will internally generate an appropriate X matrix specifying the group structure from this factor information, so no additional data are required. However, if a canonical correlation-type analysis is to be done, then a separate data sheet containing one or more X variables (and having the same number and labels for the samples as the resemblance matrix) needs to be identified. The mechanics of performing a CAP analysis are described by the following steps (Fig. 5.2):

  1. First, principal coordinates are obtained from the resemblance matrix to describe the cloud of multivariate data in Euclidean space (see Fig. 3.1 for details). The individual PCO axes are not, however, standardised by their eigenvalues. Instead, they are left in their raw (orthonormal100) form, which we will denote by Q$^0$. This means that not only is each PCO axis independent of all other PCO axes, but also each axis has a sum-of-squares (or length) equal to 1. So, the PCO data cloud is effectively “sphericised” (see the section entitled Sphericising variables).

  2. From matrix X, calculate the “hat” matrix H = X[X′X]–1X′. This is the matrix derived from the solutions to the normal equations ordinarily used in multiple regression (e.g., Johnson & Wichern (1992) , Neter, Kutner, Nachtsheim et al. (1996) )101. Its purpose here is to orthonormalise (“sphericise”) the data cloud corresponding to matrix X as well.

  3. If the resemblance matrix is N × N, then there will be, at most, (N – 1) non-zero PCO axes. If we did the canonical analysis using all of these axes, it would be like trying to fit a model to N points using (N – 1) parameters, and the fit would be perfect, even if the points were completely random and the hypothesis were false! So, only a subset of m < (N – 1) PCO axes should be used, denoted by Q$^0 _ m$. The value of m is chosen using appropriate diagnostics (see the section Diagnostics).

  4. A classical canonical analysis is done to relate the subset of m orthonormal PCO axes to X. This is done by constructing the matrix Q$^0 _ m$′HQ$^0 _ m$. Eigenvalue decomposition of this matrix yields canonical eigenvalues $\delta _1^2$, $\delta _2^2$,$\ldots \delta _s^2$ and their associated eigenvectors. The trace of matrix Q$^0 _ m$′HQ$^0 _ m$ is equal to the sum of the canonical eigenvalues. These canonical eigenvalues are also the squared canonical correlations. They indicate the strength of the association between the data cloud and the hypothesis of interest.

  5. The canonical coordinate axis scores C, a matrix of dimension (N × s), are used to produce the the CAP plot. These are made by pre-multiplying the eigenvectors by Q$^0 _ m$ and then scaling (multiplying) each of these by the square root of their corresponding eigenvalue. Thus, the CAP axes are linear combinations of the orthonormal PCO axes.
     

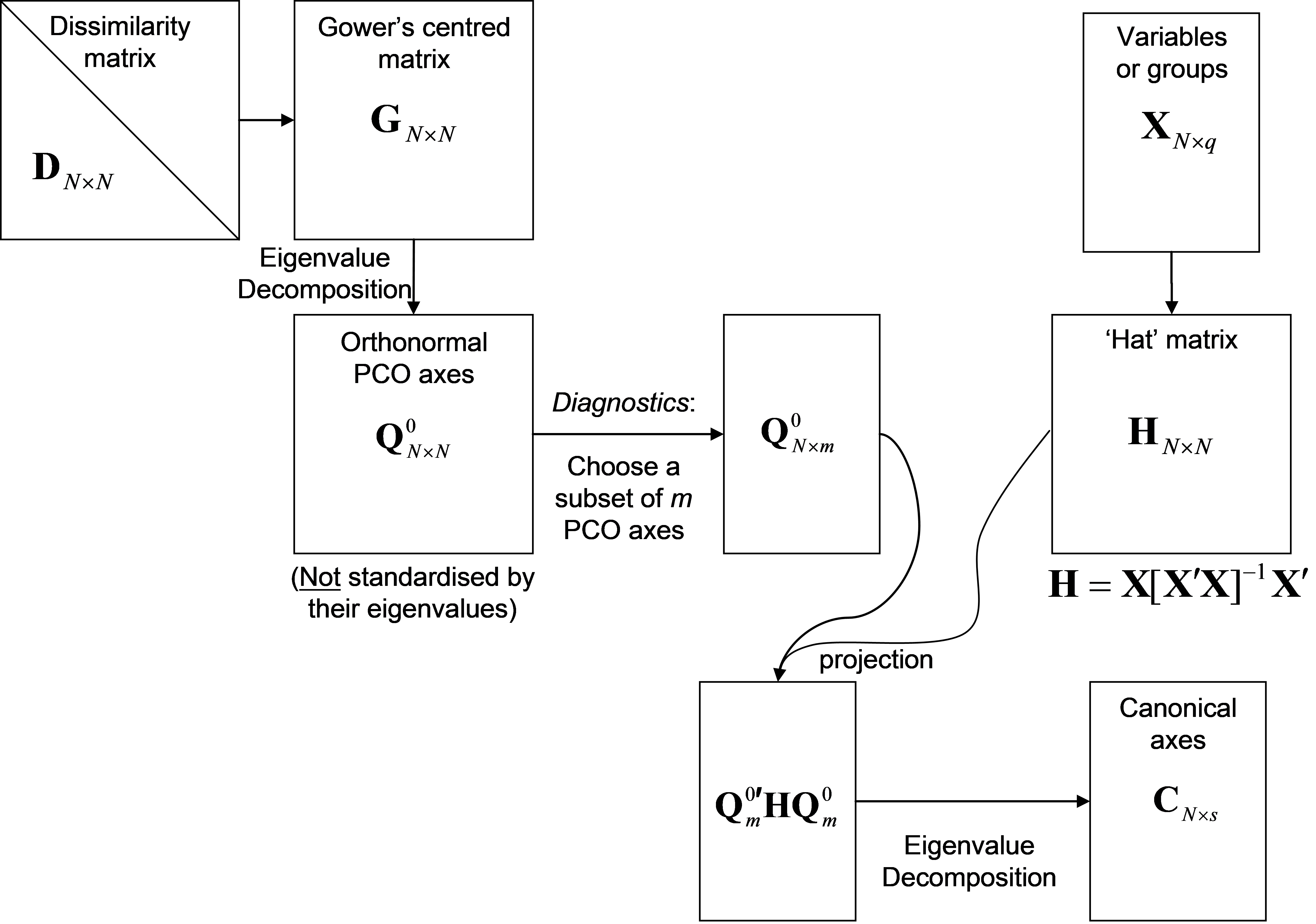Fig5.2.png Fig. 5.2. Schematic diagram of the steps involved in performing a CAP analysis.

The number of canonical axes produced by the analysis (= s) will be the minimum of (m, q, (N – 1)). For a canonical correlation-type analysis, q is the number of variables in X. For a discriminant analysis, q = (g – 1), where g is the number of groups. If the analysis if based on Euclidean distances to begin with, then CAP is equivalent to classical canonical discriminant analysis (CDA) or canonical correlation analysis (CCorA). In such cases, the number for m should be chosen to be the same as the number of original variables (p) in data matrix Y, except in the event that p is larger than (N – 1), in which case the usual diagnostics should be used to choose m.

99 If a resemblance matrix of similarities is available instead, then the CAP routine in PERMANOVA+ will automatically transform these into dissimilarities before proceeding; the user need not do this as a separate step.

100 Orthonormal axes are uncorrelated and have a sum-of-squares and cross-products matrix (SSCP) equal to the identity matrix I (all sums of squares = 1 and all cross-products = 0).

101 CAP automatically centres the X data cloud.

Back to top