5.14 CAP versus dbRDA
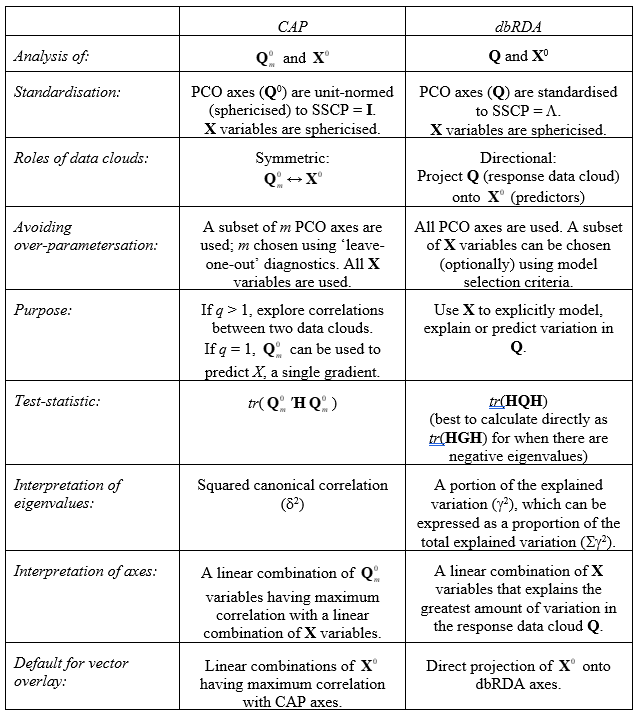
So, how does CAP differ from dbRDA for relating two sets of variables? First, dbRDA is directional. Each set of variables has a role as either predictor variables (X) or response variables (Q), while for CAP (when there are multiple variables in X), the two sets of variables are essentially treated symmetrically. Canonical correlation analysis (on the basis of Euclidean distances) finds linear combinations of Y and linear combinations of X that are maximally correlated with one another. In contrast, RDA finds linear combinations of X that are best at explaining or predicting Y (the latter set of variables are not sphericised). Note that canonical correlation sphericises both of the data clouds using X$^0$ and Y$^0$ in the calculations. This ensures that the correlations among the variables within either set are taken into account. In contrast, RDA uses sphericised X$^0$ (by constructing matrix H), but the variables in Y are not sphericised. Now, CAP generalises canonical correlation to any resemblance measure by replacing Y$^0$ with Q$^0 _m$, while dbRDA generalises RDA to any resemblance measure by replacing Y with Q. Furthermore, no matter how many variables occurred in the original Y matrix, over-parameterisation in CAP can be avoided by a prudent choice for m (generally obtained using diagnostics).
The decision of which method to use should always be based on the conceptual goals of the analysis. When there are multiple X variables, CAP can be helpful for exploring relationships between these variables and a multivariate data cloud expressed by a resemblance matrix. In contrast, dbRDA is more appropriate when one wishes to explicitly model the variability in the multivariate data cloud using a set of X predictor variables. Table 5.1 provides a summary of the differences between these two approaches.
Table 5.1. Summary of differences between CAP and dbRDA for the analysis of the relationships between two sets of variables. Matrices are defined in the text and are also defined in the index of mathematical notation.