1.3 Huygens’ theorem
This partitioning is fine and perfectly valid for Euclidean distances. But what happens if we wish to base the analysis on some other dissimilarity (or similarity) measure? This is important because Euclidean distance is generally regarded as inappropriate for analysing ecological species abundance data6, especially because of its lack of emphasis on species composition (e.g., Faith, Minchin & Belbin (1987) , Legendre & Legendre (1998) , Clarke (1993) , Clarke, Somerfield & Chapman (2006) ). Other measures, such as Bray-Curtis ( Bray & Curtis (1957) ), Kulczynski (see Faith, Minchin & Belbin (1987) ), Jaccard (see Legendre & Legendre (1998) ), binomial deviance ( Anderson & Millar (2004) ), Hellinger ( Rao (1995) ) or a modified Gower measure ( Anderson, Ellingsen & McArdle (2006) ), may be more appropriate, in different situations, for analysing community data. Although analyses on the basis of some measures (such as chi-squared or Hellinger) can be achieved by applying Euclidean distances to data that have been transformed in a particular way (see Legendre & Gallagher (2001) for details), we wish to retain the full flexibility of methods like ANOSIM or MDS and allow the analysis to be based on any reasonable distance or dissimilarity measure of choice.
Unfortunately, for many resemblance measures favoured by ecologists, we cannot easily calculate distances to centroids. The reason for this is that the sample centroid (the point lying in the centre of the data cloud) in the space defined by these measures will not be the same as the vector of arithmetic averages for each variable. It is actually quite unclear just how one could go about calculating centroids for the majority of these non-Euclidean measures on the basis of the raw data alone. Thus, for these situations, we shall instead rely on what is known as Huygens’ theorem7 (Fig. 1.3). This theorem states (for Euclidean space) that the sum of squared distances from individual points to their group centroid is equal to the sum of squared inter-point distances, divided by the number of points in the group (e.g., Legendre & Anderson (1999) , see Appendix B therein).
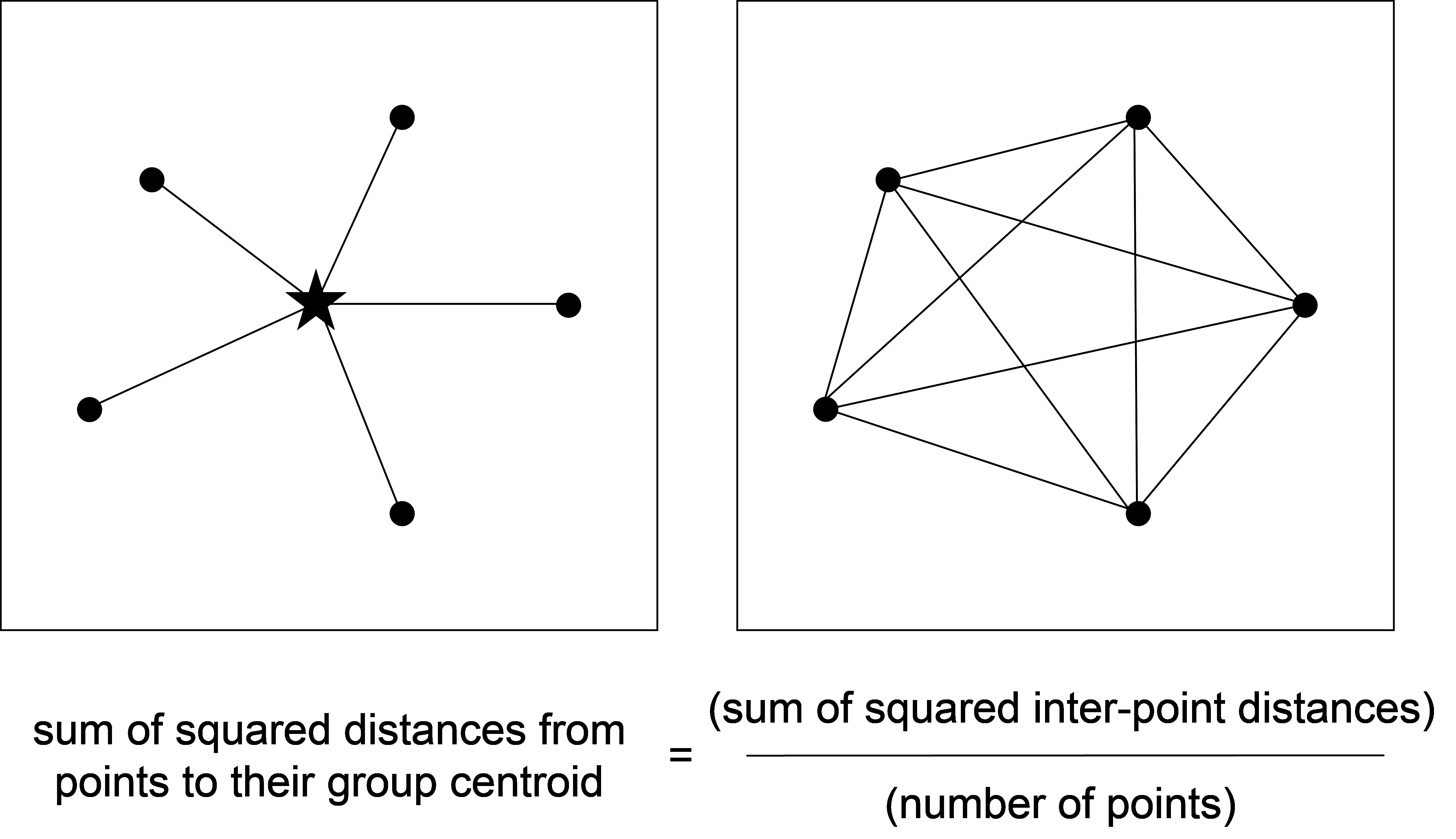Fig. 1.3. Schematic diagram of Huygens’ theorem.
This theorem appears to be very simple, and it is. In fact, it is perfectly safe to calculate these two quantities using Euclidean distances and you are encouraged to try a simple example (say in two dimensions) to prove it to yourself. Importantly, what it means for us is that we can use the inter-point distances (or dissimilarities) alone in order to calculate the sums of squares, without ever having to calculate the position of the centroids at all! Therefore, for the cases where we cannot calculate centroids directly (i.e., for most dissimilarity measures), we can use the inter-point values instead to do the partitioning. The only properties required of our dissimilarity measure in order to use this approach are that it be non-negative, symmetric (the distance or dissimilarity from point A to point B must be the same as from point B to point A), and that all self dissimilarities (from point A to itself) be zero. Virtually all measures that are worth using possess these three properties8.
6 See Warton & Hudson (2004) for an alternative point of view and counter-argument to this assumption.
7 Christian Huygens (1629-1695) was a Dutch mathematician, astronomer and physicist, famous for, among other things, patenting the first pendulum clock.
8 The mathematical and geometric properties of dissimilarity measures are reviewed by Gower & Legendre (1986) .