1.16 Additivity
Central to an understanding of what an interaction means for linear models25 is the idea of additivity. Consider the example of a two-way crossed design for a univariate response variable, where the cell means and marginal means are as shown in Fig. 1.19a. Note that the marginal means are the means of the levels of each factor ignoring the other factor. In an additive model, the difference between two levels of a factor (say between B1 and B2) between individual cells (i.e., within each level of A, that is to say, within each column) are equal to the differences in the marginal means (i.e., the difference between the mean of B1 and B2 if factor A were to be ignored). This can be contrasted with the situation where the differences in cell means are quite different from the differences in marginal means (e.g., Fig. 1.19b), in which case, there is an interaction between the factors. So, this is another way to articulate what is meant by a significant interaction: effects of factors within levels of other factors are non-additive and thus do not match the corresponding shifts in marginal means. The interaction term, in fact, measures the deviation of the cell means we actually got from what we would expect them to be if they were to follow the marginal means, as would be the case if the effects of the two factors were purely additive.
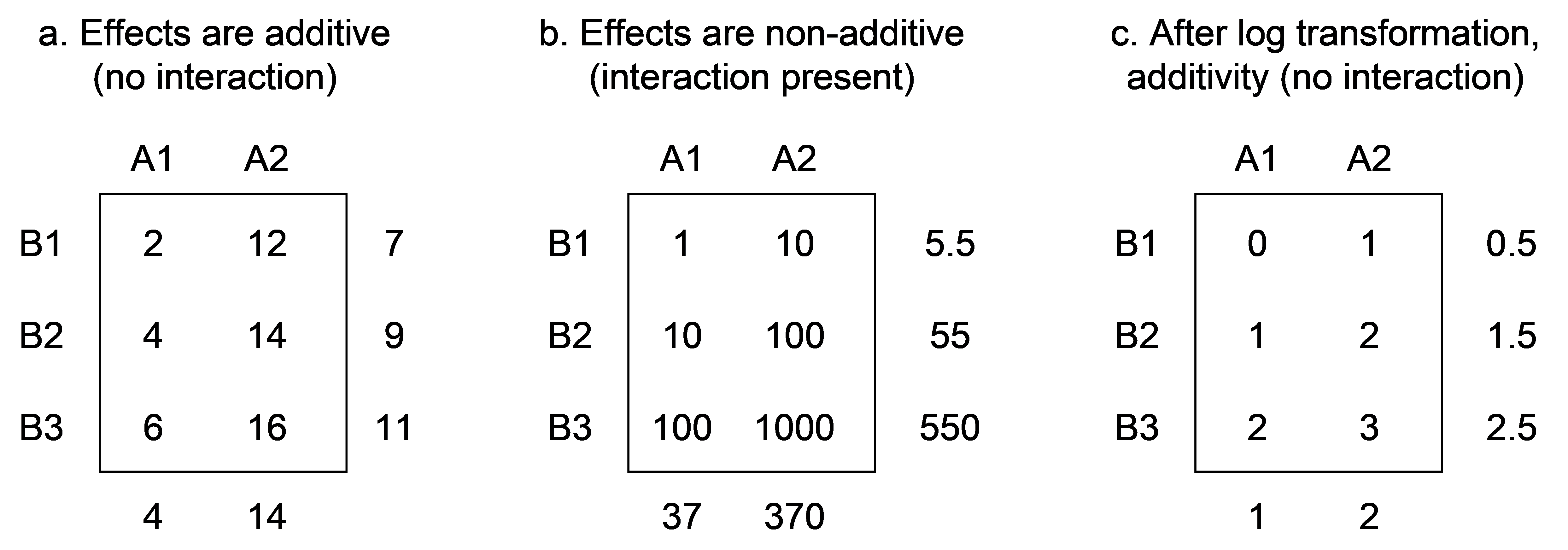Fig. 1.19. Marginal and cell means for a univariate crossed design showing examples of (a) additive effects, (b) multiplicative effects and (c) additivity after log10-transformation of (b).
Clearly, the additivity (or not) of the effects of factors is also going to depend on whether or not the data have been transformed (or standardised or ranked) prior to analysis. This is as true for multivariate data as it is for univariate data. For example, if a log (base 10) transformation is applied to the means shown in Fig. 1.19b, then we would have an additive model with no significant interaction (Fig. 1.19c). Such a situation typifies phenomena where the true effects are multiplicative, rather than being additive. In univariate analysis, transformations can often be used to remove significant interaction terms, yielding additivity ( Tukey (1947) , Box & Cox (1964) , Kruskal (1965) , Winsberg & Ramsay (1980) ).
For multivariate analysis of ecological data, however, transformations are usually applied neither to fulfill assumptions, nor in order to remove significant interactions, but rather as a method of changing the relative emphasis of the analysis on rare versus more abundant species (e.g., Clarke & Green (1988) , Clarke & Warwick (2001) ). In PRIMER, a blanket transformation can be applied to all variables by choosing Analyse > Pre-treatment > Transform (overall) and then choosing from a range, in increasing severity, from no transformation, square root, fourth root or log(x+1) down to a reduction of the values to binary presence (1) or absence (0). An approach using an intermediate-level transformation (square root or fourth root) has been recommended as a way to reduce the contribution of highly abundant species in relation to less abundant ones in the calculation of the Bray-Curtis measure; rare species will contribute more, the more severe the transformation ( Clarke & Green (1988) , Clarke & Warwick (2001) ).
In addition to the transformation, additivity of effects in multivariate analysis is also going to depend on whether or not the dissimilarities are ranked before analysis (yet another reason why patterns in a non-metric MDS, which preserves ranks only, may not necessarily clearly reflect what is given in the PERMANOVA output). The choice of dissimilarity measure itself is also very important here. By performing the partitioning, PERMANOVA is effectively applying a linear model to a multivariate data cloud, as defined by these choices. So the presence of a significant interaction (or not) by PERMANOVA will naturally depend on them. Nevertheless, the choice of an appropriate dissimilarity measure (and also the choice of transformation, if any) should genuinely be driven by the biology and ecology (or other nature) of the system being studied and what is appropriate regarding your hypotheses, and not by reference to these statistical issues (unlike typical traditional univariate ANOVA).
25 The ANOVA models analysed by PERMANOVA are linear only in the space of the multivariate cloud defined by the dissimilarity measure of choice; they are not linear in the space of the original variables (unless the resemblance measure chosen was Euclidean distance).