1.7 Assumptions
Recall that for traditional one-way ANOVA, the assumptions are that the errors are independent, that they are normally distributed with a mean of zero and a common variance, and that they are added to the treatment effects. In the case of a one-way analysis, the PERMANOVA test using permutations assumes only that the samples are exchangeable under a true null hypothesis12. The assumption of exchangeability is tantamount to assuming that the multivariate observations (samples) are independent and identically distributed (i.i.d.) under a true null hypothesis. Thus, although there are no explicit assumptions regarding the distributions of the original variables (they are certainly not assumed to be normally distributed), independence and homogeneity of dispersions (in the space of the resemblance measure) are directly implied by the permutation procedure. Clearly, if samples have very different dispersions in different groups, then they are not really exchangeable. Also, if the samples are unequally correlated with one another (e.g., temporally or spatially), then randomly shuffling them will destroy this kind of inherent structure. In contrast, it is not expected that the individual variables which have been measured on the same samples (in the multivariate case) are independent of one another and this is not assumed. When permutations are done, the values for different variables within a sample are kept together as a unit, so whatever correlation structure there might be among the variables is not altered under permutation.
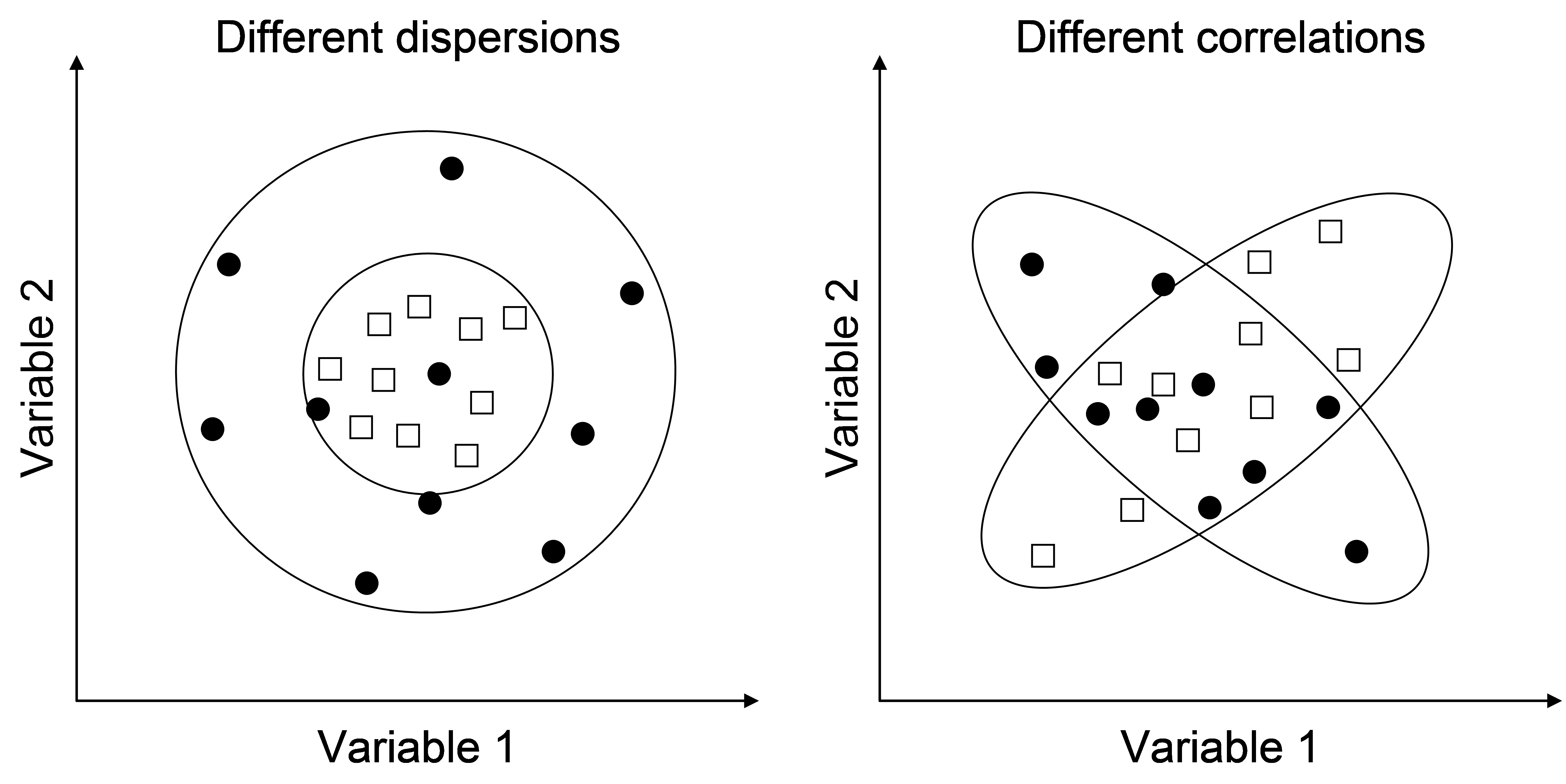Fig. 1.6. PERMANOVA will be sensitive to differences in dispersions (left) but not differences in correlation structure (right) among groups.
PERMANOVA, like ANOSIM ( Clarke (1993) ), will be sensitive to differences in dispersion among groups (Fig. 1.6). Indeed, the construction of pseudo-F ratios in PERMANOVA uses pooled estimates of within-group variability, so homogeneity of multivariate dispersions is also implicit in the partitioning. A separate test for homogeneity of dispersions, using the PERMDISP routine (see chapter 2) can be done prior to performing PERMANOVA (or, indeed, to investigate the null hypothesis of homogeneity in its own right). However, we consider that a non-significant result from PERMDISP is not strictly necessary to achieve prior to using PERMANOVA. It is likely that PERMDISP will detect differences in dispersion that, in many cases, are not substantial enough to “de-rail” (i.e. to inflate the error rates of) the PERMANOVA test13. This is analogous to the situation in univariate analysis; traditional ANOVA is quite robust to many forms of heterogeneity, especially with large sample sizes ( Box (1953) ). Instead, we can consider the homogeneity of dispersions to be included as part of the general null hypothesis of “no differences” among groups being tested by PERMANOVA (even though the focus of the PERMANOVA test is to detect location effects). If significant heterogeneity were detected by PERMDISP and differences among groups were also detected using PERMANOVA, then the latter could have been caused by differences in location, differences in dispersion, or some combination of the two. Thus, performing a test using PERMDISP, as well as examining the average within and between-group dissimilarities and the position of samples from different groups in unconstrained ordination plots (MDS or PCO), will help to uncover the nature of any differences among groups detected by PERMANOVA.
Unlike many of the traditional MANOVA test statistics (e.g., Mardia, Kent & Bibby (1979) , Seber (1984) ), PERMANOVA will not be sensitive, however, to differences in correlation structure among groups (Fig. 1.6). See Krzanowski (1993) for a permutation test designed to compare correlation structures among variables across different groups.
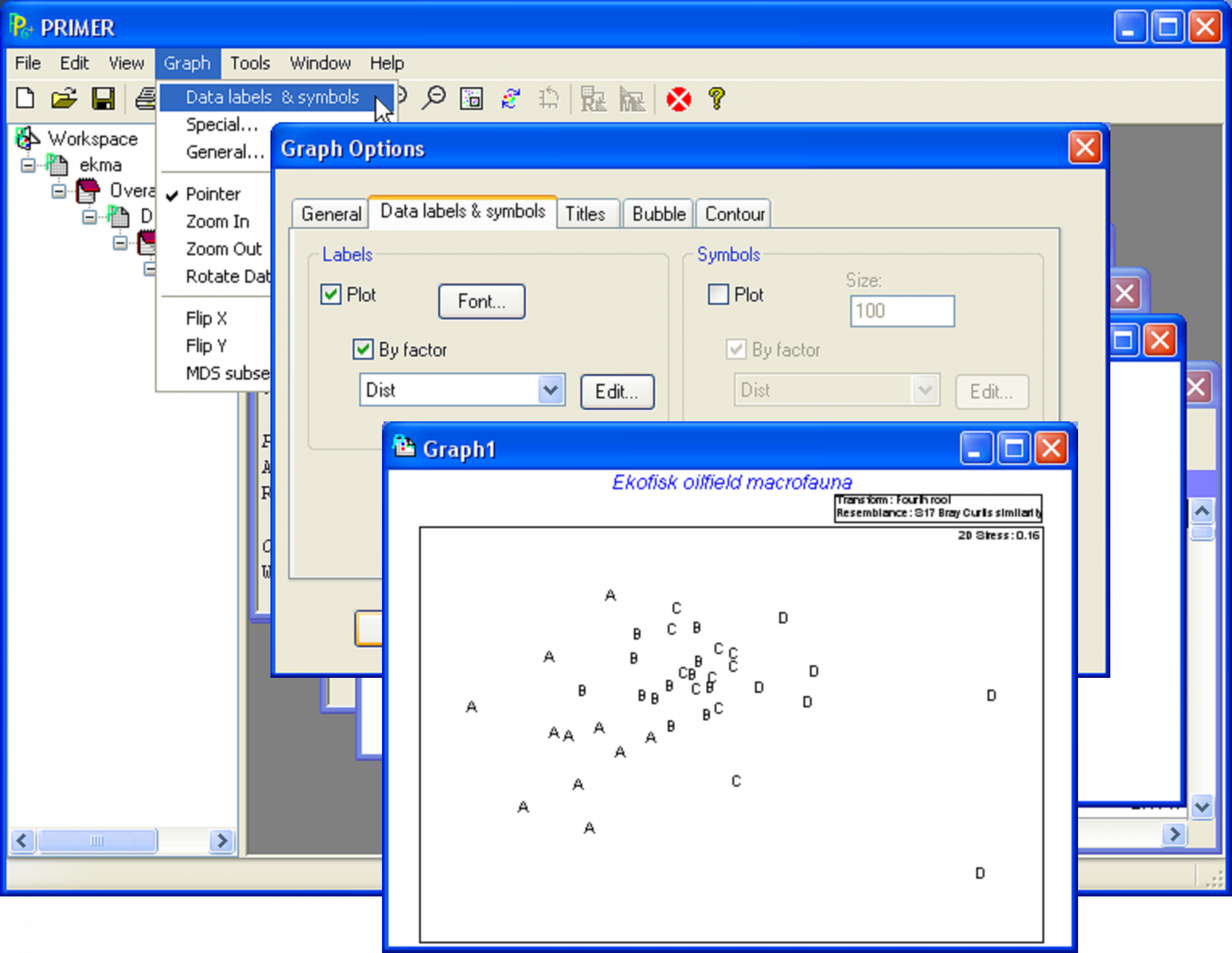Fig. 1.7. Producing an MDS plot of the Ekofisk macrofauna data.
12 Exchangeability of multivariate observations (samples) is assured if we have done a random allocation of sample units to groups or treatments a priori ( Fisher (1935) ). For observational studies, where we cannot do this (i.e., the groups already occur in nature and we draw a random sample from them), we must assume exchangeability under a true null hypothesis ( Kempthorne (1966) ).
13 Certainly a worthy topic for future study is to discover the conditions under which PERMANOVA will show inflated rates of either Type I or Type II error in the face of heterogeneity in the distributions of multivariate samples among groups.