1.4 Sums of squares from a distance matrix

We can now consider the structure of a distance/dissimilarity matrix and how sums of squares for a one-way multivariate ANOVA partitioning would be calculated (Fig. 1.4).

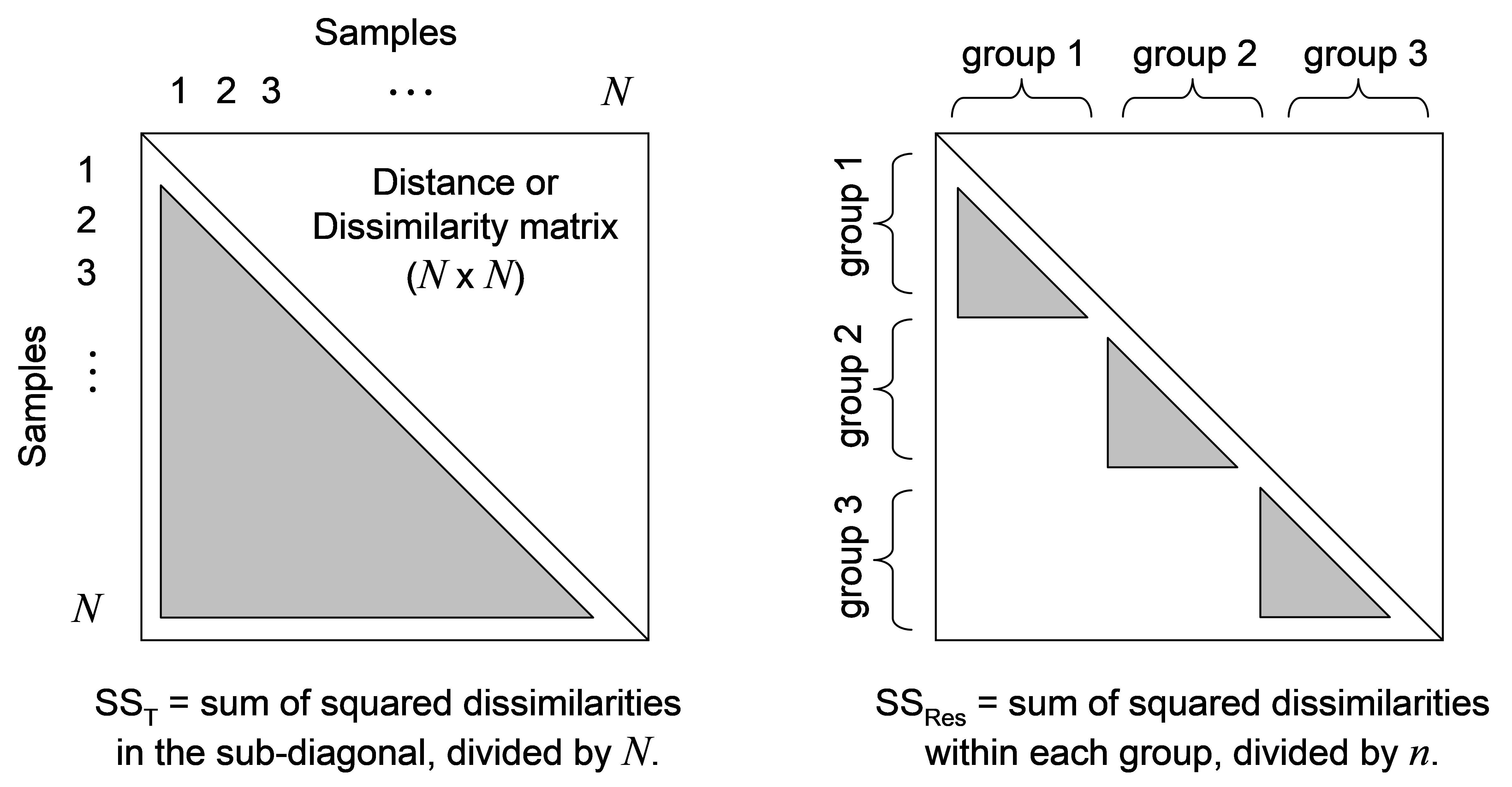Fig. 1.4. Calculation of sums of squares directly from a distance/dissimilarity matrix.

If we let $d _ {ij}$ be the dissimilarity (or distance) between sample i and sample j, then the total sum of squares is the sum of the inter-point dissimilarities among all samples, divided by N:

$$ SS _ T = \frac{1}{N} \sum _ {i=1} ^ {N-1} \sum _ {j=i+1} ^ {N} d _ {ij} ^2 \tag{1.1} $$

and the residual (within-group) sum of squares (assuming, for now, a balanced design having an equal sample size of n per group) is:

$$ SS _ {Res} = \frac{1}{n} \sum _ {i=1} ^ {N-1} \sum _ {j=i+1} ^ {N} d _ {ij} ^2 \omega _ {ij} \tag{1.2} $$

where $\omega _ {ij}$ takes the value of 1 if samples i and j are in the same group, otherwise it takes the value of zero. This amounts to adding up the squares of all the dissimilarities between samples that occur within the same group. These quantities are shown schematically in Fig. 1.4. The among-group sum of squares can also be calculated directly or, more simply, as the difference: $SS _A = SS _T - SS _ {Res}$. Partitioning of distance matrices having Euclidean metric properties according to ANOVA experimental designs has been discussed previously by Edgington (1995) , Pillar & Orloci (1996) and Excoffier, Smouse & Quattro (1992) , whereas Gower & Krzanowski (1999) extended this idea to semi-metric dissimilarities having only the properties of symmetry (i.e., $d _{ij} = d _{ji}$) and that $d _ {ij} \ge 0$ and $d _ {ii} = 0$ for all samples.

A related point is that PERMANOVA (or any of the other methods that partition variability in the routines offered by the PERMANOVA+ add-on) does not suffer from the problems recently identified by Legendre, Borcard & Peres-Neto (2005) for the Mantel and partial Mantel test ( Mantel (1967) , Smouse, Long & Sokal (1986) )⁹. Confusion might arise because Legendre, Borcard & Peres-Neto (2005) used the words “variation partitioning on distance matrices” to describe the general Mantel approach. PERMANOVA, however, is not a Mantel test. The essential issue regarding the partial Mantel approach (known for some time to be potentially problematic, see Dutilleul, Stockwell, Frigon et al. (2000) , Legendre (2000) , Raufaste & Rousset (2001) and Rousset (2002) ) is that it works on “unwound” distance matrices, where inter-point distance values are treated independently as a single vector. In contrast, the methods in the PERMANOVA+ add-on all work on the distance/dissimilarity matrix directly but, importantly, they retain its inherent structure; the values in the matrix are not unwound nor are they treated or modelled as independent of one another. The PERMANOVA+ methods are therefore directly akin to the so-called “canonical partitioning” methods referred to by Legendre, Borcard & Peres-Neto (2005) , and are correct for partitioning and analysing the actual variability inherent in multivariate data clouds.

---

⁹ The original simple Mantel test ( Mantel (1967) ) to relate two distance matrices, from which several of the PRIMER routines (RELATE, BIOENV, BEST, BVSTEP and 2-stage MDS) all drew some inspiration, is valid and does have utility in appropriate applications, as pointed out by Legendre, Borcard & Peres-Neto (2005) .