11.2 Example: Garroch Head macrofauna

For the 12 sampling stations (Fig. 8.3) across the sewage-sludge dump ground at Garroch Head {G}, the biotic information was supplemented by sediment chemical data on metal concentrations (Cu, Mn, Co, ...) and organic loading (% carbon and nitrogen); also recorded was the water depth at each station. The data matrix is shown in Table 11.1; it follows the normal convention in classical multivariate analysis of the variables appearing as columns and the samples as rows.^¶
 

Table 11.1. Garroch Head dump ground {G}. Sediment metal concentrations (ppm), water depth at the site (m) and organic loading of the sediment (% carbon and nitrogen), for the transect of 12 stations across the sewage-sludge dump site (centre at station 6), see Fig. 8.3.

Station	Cu	Mn	Co	Ni	Zn	Cd	Pb	Cr	Dep	%C	%N
1	26	2470	14	34	160	0	70	53	144	3	0.53
2	30	1170	15	32	156	0.2	59	15	152	3	0.46
3	37	394	12	38	182	0.2	81	77	140	2.9	0.36
4	74	349	12	41	227	0.5	97	113	106	3.7	0.46
5	115	317	10	37	329	2.2	137	177	112	5.6	0.69
6	344	221	10	37	652	5.7	319	314	82	11.2	1.07
7	194	257	11	34	425	3.7	175	227	74	7.1	0.72
8	127	246	10	33	292	2.2	130	182	70	6.8	0.58
9	36	194	6	16	89	0.4	42	57	64	1.9	0.29
10	30	326	11	26	108	0.1	44	52	80	3.2	0.38
11	24	439	12	34	119	0.1	58	36	83	2.1	0.35
12	22	801	12	33	118	0	52	51	83	2.3	0.45

 

No replication is available for the 12 stations so the variance-to-mean plots suggested in Chapter 9 are not possible, but simple scatter plots of all pairwise combinations of variables (draftsman plots, see the later Fig. 11.9) suggest that log transformations are appropriate for the concentration variables, though not for water depth. The criteria here are that variables should not show marked skewness across the samples, enabling meaningful normalisation, and that the relationships between them should be approximately linear; the standard product-moment correlations between variables and Euclidean distances between samples are then satisfactory summaries. In pursuit of this, note that whilst each variable could in theory be subjected to a different transformation it is more logical to apply the same transformation to all variables of the same type. Thus the decision to log all the metal data stems not just from the draftsman plots but also from previous experience that such concentration variables often have standard deviations proportional to their means; i.e. a roughly constant percentage variation is log transformed to a stable absolute variance.

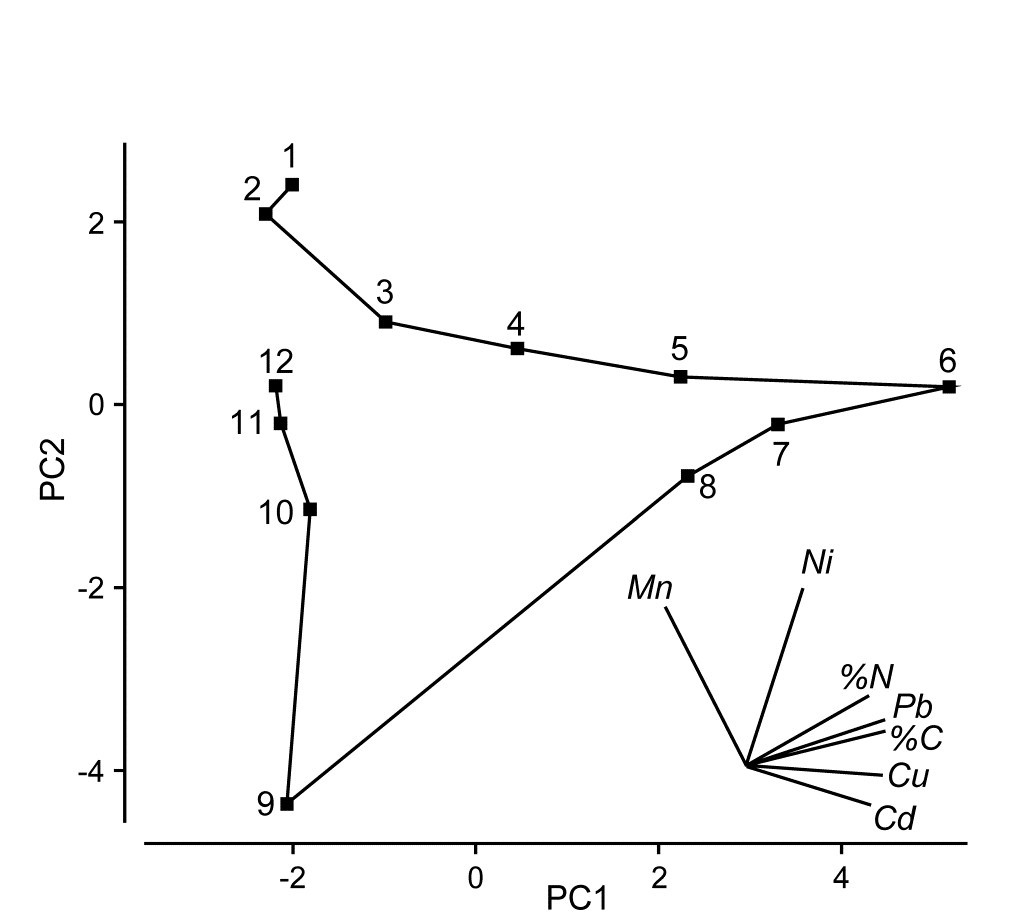
Fig. 11.1 displays the first two axes (PC1 and PC2) of a PCA ordination on the transformed data of Table 11.1. In fact, the first component accounts for much of the variability (61%) in the full matrix, and the second a further 27%, so the first two components account for 88% and the 2-d plot provides an accurate summary of the relationships. The axes are defined as

$$ PC1 = 0.38 Cu ^ \prime – 0.22 Mn ^ \prime – 0.08 Co ^ \prime + 0.15 Ni ^ \prime + 0.37 Zn ^ \prime + 0.33 Cd ^ \prime + 0.37 Pb ^ \prime + 0.35 Cr ^ \prime $$ $$ – 0.12 Dep ^ \prime + 0.37 C ^ \prime + 0.33 N ^ \prime \tag{11.1} $$ $$ PC2 = -0.04 Cu ^ \prime + 0.42 Mn ^ \prime +0.54 Co ^ \prime + 0.47 Ni ^ \prime + 0.16 Zn ^ \prime -0.11 Cd ^ \prime + 0.13 Pb ^ \prime - 0.09 Cr ^ \prime $$ $$ +0.46 Dep ^ \prime + 0.09 C ^ \prime + 0.19 N ^ \prime $$

Broadly, PC1 represents an axis of increasing contaminant load since the sizeable coefficients are all positive. (The dash denotes that variables have been log transformed, excepting Dep, and normalised to zero mean and unit standard deviation). PC2 needs to be orthogonal to PC1 (coefficients cross-multiplying to zero) and it does this simply here by, e.g., the large PC1 coefficients being small in PC2 and vice-versa.

Fig. 11.1. Garroch Head dump ground {G}. Two-dimensional PCA ordination of the 11 environmental variables of Table 11.1 (transformed and normalised), for the stations (1–12) across the sewage-sludge dump site centred at station 6 (% variance explained = 88%). Selected vectors are shown; they represent direction and relative strength of linear increase of normalised variables in this 2-d plane (‘base variables’ option). Only the directions of vectors should be interpreted; their location is arbitrary.
 

Fig. 11.1 shows a strong pattern of change on moving from the ends of the transect to the dump site centre, which (unsurprisingly) has the greatest levels of organic enrichment and metal concentrations (exceptions are Mn$^ \prime$, Co$^ \prime$ and Ni$^ \prime$). The superimposed vectors are in this case entirely accurate (see the footnote on p7-19), since equation (11.1) shows that the axes are linear in the variables. For example, the Cu$^ \prime$ vector is pointing along the x axis (to the right) because it has a sizeable positive coefficient of 0.38 on PC1, and only slightly downwards because of its small negative coefficient (-0.04) on the PC2 axis, whereas Mn$^ \prime$ and Ni$^ \prime$ increase strongly up the y axis (i.e. one would expect Ni$^ \prime$ to be at its lowest for site 9), with Mn$^ \prime$ pointing left and Ni$^ \prime$ right because of their (smaller) negative and positive PC1 terms. %C and Pb vectors are coincident, at least on these 2 axes, from their near identical coefficients.

---

^¶ This is in contrast with abundance matrices which, because of their often larger number of variables (species) are usually transposed, i.e. the samples are displayed as columns. The PRIMER software package handles data entered either way round, of course, though it is important to specify in the entry dialog whether the rows or the columns should be taken as samples.