15.5 Model matrices & ‘RELATE’ tests

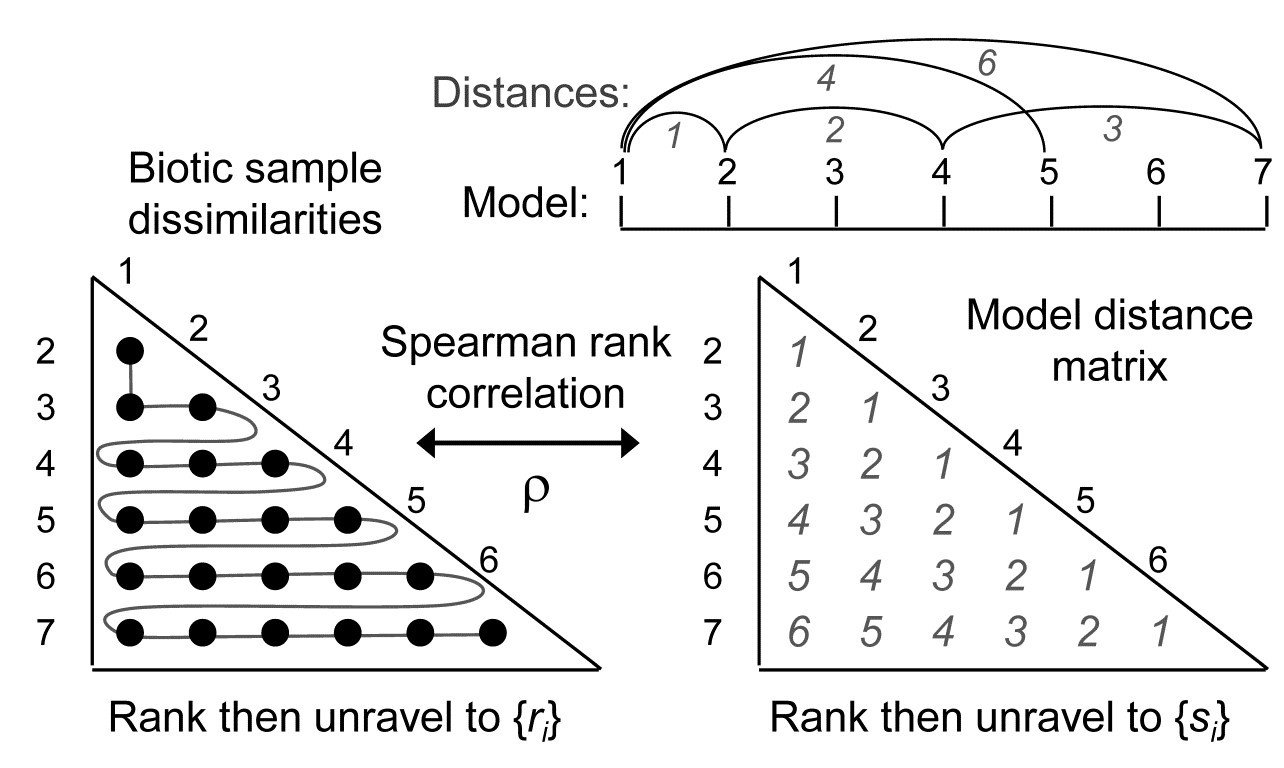
The form of the seriation statistic is simply a matrix correlation coefficient (e.g. equation 11.3) between the unravelled entries of the similarity matrix of the biotic samples and a model distance matrix defined, in this case from equi-spaced points on a line:

Correlation coefficients available with the PRIMER RELATE routine are three non-parametric options: Spearman, equation (11.3); Kendall’s $\tau$ ( Kendall (1970) ); weighted Spearman (11.4); and one measure which uses the similarities themselves rather than their ranks: the standard product-moment or Pearson correlation, (2.3). The latter is the form of matrix correlation first defined by Mantel (1967) , in an epidemiological context. The Spearman coefficient $\rho$ is a natural choice for our rank-based philosophy and has an interesting affinity with the ordered ANOSIM statistic, $R ^ O$, discussed on page 6.10, which builds the same model matrix of serial trend (with or without replication, see later). This can, of course, be seriation in time rather than space, so this form of RELATE test provides a useful means of testing and quantifying the extent of a time trend – perhaps an inter-annual drift away of an assemblage from its initial state, through gradual processes such as climate change.