9.3 Multivariate case
There being no necessity to transform to attain distributional properties, transformations play an entirely separate (but equally important) role in the clustering and ordination methods of the previous chapters, that of defining the balance between contributions from common and rarer species in the measure of similarity of two samples.
Returning to the simple example of Chapter 2, a subset of the Loch Linnhe macrofauna data, Table 9.3 shows the effect of a 4th root transformation of these abundances on the Bray-Curtis similarities. The rank order of the similarity values is certainly changed from the untransformed case, and one way of demonstrating how dominated the latter is by the single most numerous species (Capitella capitata) is shown in Table 9.4. Leaving out each of the species in turn, the Bray-Curtis similarity between samples 2 and 4 fluctuates wildly when Capitella is omitted in the untransformed case, though changes much less dramatically under 4th root transformation, which downweights the effect of single species.
Table 9.3. Loch Linnhe macrofauna {L} subset. Untransformed and 4th root-transformed abundances for some selected species and samples (years), and the resulting Bray-Curtis similarities between samples.
| Untransformed | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample: | 1 | 2 | 3 | 4 | ||||||
| Species | Sample | 1 | 2 | 3 | 4 | |||||
| Echinoca. | 9 | 0 | 0 | 0 | 1 |
– | ||||
| Myrioche. | 19 | 0 | 0 | 3 | 2 |
8 | – | |||
| Labidopl. | 9 | 37 | 0 | 10 | 3 |
0 | 42 | – | ||
| Amaeana | 0 | 12 | 144 | 9 | 4 |
39 | 21 | 4 | – | |
| Capitella | 0 | 128 | 344 | 2 | ||||||
| Mytilus | 0 | 0 | 0 | 0 | ||||||
| $\sqrt{} \sqrt{}$-transformed | ||||||||||
| Sample: | 1 | 2 | 3 | 4 | ||||||
| Species | Sample | 1 | 2 | 3 | 4 | |||||
| Echinoca. | 1.7 | 0 | 0 | 0 | 1 |
– | ||||
| Myrioche. | 2.1 | 0 | 0 | 1.3 | 2 |
26 | – | |||
| Labidopl. | 1.7 | 2.5 | 0 | 1.8 | 3 |
0 | 68 | – | ||
| Amaeana | 0 | 1.9 | 3.5 | 1.7 | 4 |
52 | 68 | 42 | – | |
| Capitella | 0 | 3.4 | 4.3 | 1.2 | ||||||
| Mytilus | 0 | 0 | 0 | 0 |
Transformation sequence
The previous remarks about the family of power transformations apply equally here: they provide a continuum of effect from $\lambda = 1$ (no transform), for which only the common species contribute to the similarity, through $\lambda = 0.5$ (square root), which allows the intermediate abundance species to play a part, to $\lambda = 0.25$ (4th root), which takes some account also of rarer species. As noted earlier, $\lambda \rightarrow 0$ can be thought of as equivalent to the $\log _ e (y)$ transformation and the latter would therefore be more severe than the 4th root transform. However, in this form, the transformation is impractical because the (many) zero values produce $\log(0) \rightarrow - \infty$. Thus, common practice is to use $\log(1+y)$ rather than $\log(y)$, since $\log(1+y)$ is always positive for positive $y$ and $\log(1+y)= 0$ for $y = 0$. The modified transformation no longer falls strictly within the power sequence; on large abundances it does produce a more severe transformation than the 4th root but for small abundances it is less severe than the 4th root. In fact, there are rarely any practical differences between cluster and ordination results performed following $y ^ {0.25}$ or $\log(1+y)$ transformations; they are effectively equivalent in focusing attention on patterns within the whole community, mixing contributions from both common and rare species.¶
Table 9.4. Loch Linnhe macrofauna {L} subset. The changing similarity between samples 2 and 4 (of Table 9.3) as each of the six species is omitted in turn, for both untransformed and 4th root-transformed abundances.
| Species omitted: | None | 1 | 2 | 3 | 4 | 5 | 6 |
| Bray-Curtis (S): | 21 | 21 | 21 | 14 | 13 | 54 | 21 |
| $\sqrt{} \sqrt{}$-transformed | |||||||
| Species omitted: | None | 1 | 2 | 3 | 4 | 5 | 6 |
| Bray-Curtis (S): | 68 | 68 | 75 | 61 | 59 | 76 | 68 |
The logical end-point of this transformation sequence is therefore not the log transform but a reduction of the quantitative data to presence/absence, the Bray-Curtis coefficient (say) being computed on the resulting matrix of 1’s (presence) and 0’s (absence). This computation is illustrated in Table 9.5 for the subset of the Loch Linnhe macrofauna data used earlier. Comparing with Table 9.3, note that the rank order of similarities again differs, though it is closer to that for the 4th root transformation than for the untransformed data. In fact, reduction to presence/absence can be thought of as the ultimate transformation in down-weighting the effects of common species. Species which are sufficiently ubiquitous to appear in all samples (i.e. producing a 1 in all columns) clearly cannot discriminate between the samples in any way, and therefore do not contribute to the final multivariate description. The emphasis is therefore shifted firmly towards patterns in the intermediate and rarer species, the generally larger numbers of these tending to over-ride the contributions from the few numerical or biomass dominants.
Table 9.5. Loch Linnhe macrofauna {L} subset. Presence (1) or absence (0) of the six species in the four samples of Table 9.3, and the resulting Bray-Curtis similarities.
| Presence/absence | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sample: | 1 | 2 | 3 | 4 | |||||
| Species | Sample | 1 | 2 | 3 | 4 | ||||
| Echinoca. | 1 | 0 | 0 | 0 | 1 |
– | |||
| Myrioche. | 1 | 0 | 0 | 1 | 2 |
33 | – | ||
| Labidopl. | 1 | 1 | 0 | 1 | 3 |
0 | 80 | – | |
| Amaeana | 0 | 1 | 1 | 1 | 4 |
57 | 86 | 67 | – |
| Capitella | 0 | 1 | 1 | 1 | |||||
| Mytilus | 0 | 0 | 0 | 0 |
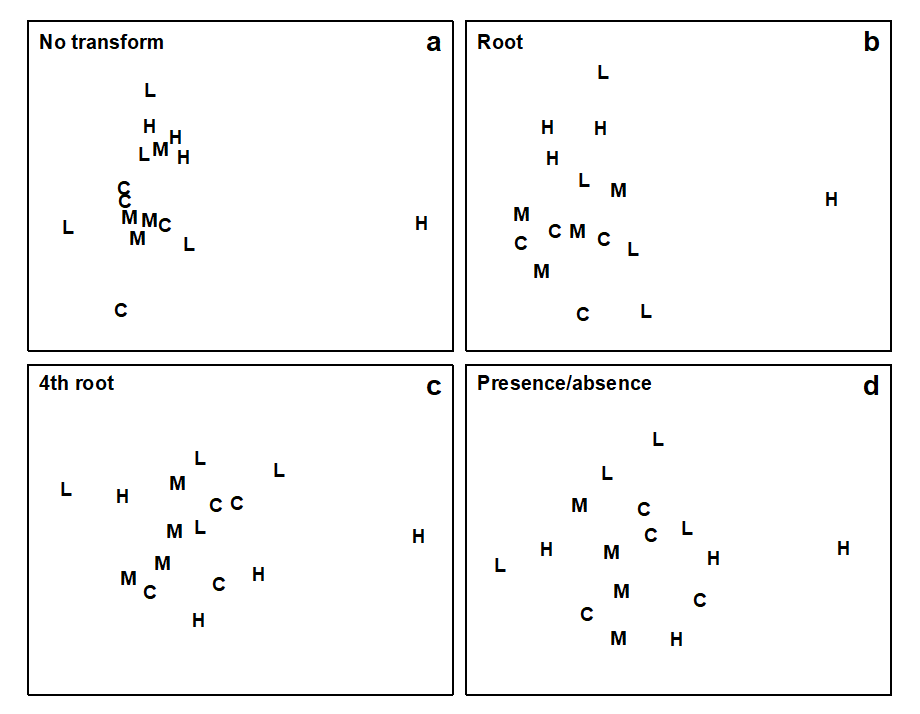
One inevitable consequence of ‘widening the franchise’ in this way, allowing many more species to have a say in determining the overall community pattern, is that it will become increasingly harder to obtain 2-d ordinations with low stress: the view we have chosen to take of the community is inherently high-dimensional. This can be seen in Fig. 9.1, for the dosing experiment {D} in the Solbergstrand mesocosm (GEEP Oslo workshop), previously met in Figs. 4.2 and 5.6. Four levels of contaminant dosing (designated Control, Low, Medium, High) were each represented by four replicate samples of the resulting nematode communities, giving the MDS ordinations of Fig. 9.1. Note that as the severity of the transformation increases, through none, root, 4th root and presence/absence (Fig. 9.1a to 9.1d respectively), the stress values rise from 0.08 to 0.19.
Fig 9.1 Dosing experiment, Solbergstrand {D}. MDS of nematode communities in four replicates from each of four treatments (C = control, L = low, M = medium, H = high dose of a hydrocarbon/copper contaminant mixture dosed to mesocosm basins), based on Bray-Curtis similarities from transformed data: a) no transform (stress = 0.08), b) $\sqrt{}$ (stress = 0.14), c) $\sqrt{} \sqrt{}$ (stress = 0.18), d) presence/absence (stress = 0.19).
It is important to realise that this is not an argument for deciding against transformation of the data. Fig. 9.1a is not a better representation of the between-sample relationships than the other plots: it is a different one. The choice of transformation is determined by which aspects of the community we wish to study. If interest is in the response of the whole community then we have to accept that it may be more difficult to capture this in a low-dimensional picture (a 3-d or higher-dimensional MDS may be desirable). On the other hand, if the data are totally dominated by one or two species, and it is these that are of key biological interest, then of course it will be possible to visualise in a 1- or 2-d picture how their numbers (or biomass) vary between samples: in that case an ordination on untransformed data will be little different from a simple scatter plot of the counts for the two main species.
¶ Though practical differences are likely to be negligible, on purely theoretical grounds it could be argued that the 4th root is the more satisfactory of the two transformations because Bray-Curtis similarity is then invariant to a scale change in y. Similarity values would be altered under a log(1+y) transformation if abundances were converted from absolute values to numbers per $m^2$ of the sampled substrate, or if biomass readings were converted from mg to g. This does not happen with a strict power transformation; it is clear from equation (2.1) that any multiplying constant applied to y will cancel on the top and bottom lines of the summations.