16.6 Comparison of resemblance measures
S Tikus Island coral cover
The use of second-stage MDS plots can be extended to also include the relative effects of choosing among different resemblance measures (similarities/dissimilarities or distances) in defining sample relationships. To illustrate this we will use area cover of 75 coral reef species on ten 30m line transects from S Tikus in the Thousand Islands, Indonesia, {I}, taken in each of the years 1981, 83, 84, 85, 87, 88, spanning a coral bleaching episode related to the 1982-3 El Niño, see Warwick, Clarke & Suharsono (1990) ; data met originally on page 6.4. Though by no means typical, the data gives a salutary lesson on the importance of selecting an appropriate resemblance measure with some care, since different coefficients result in widely differing descriptions.
The 1983 samples were notably denuded of live coral cover, with average % cover reducing by an order of magnitude and number of species more than halving. The sparsity of non-zero entries on the 1983 transects makes the Bray-Curtis dissimilarity rather unstable, with many 100% dissimilarities between transects in that year.
Clarke, Somerfield & Chapman (2006)
suggest that a modified form of Bray-Curtis could be useful in such cases.
Zero-adjusted Bray-Curtis
Two samples with small numbers of only one or two species can vary wildly in their dissimilarity, from 0% if they happen to consist of a single individual of the same species, to 100% if those two individuals are from different species. If the samples contain no species whatsoever, their Bray-Curtis dissimilarity is undefined, since it is a coefficient which ignores joint absences thus leaving no data on which to perform a calculation. (Both the numerator and denominator in equation 2.1 are zero, and 0/0 is undefined). This may be a reasonable conclusion in some contexts: if the sampler size is inadequate, and capable of missing all organisms in two quite different locations (or times or treatments), then nothing can be said about whether the communities might have been similar or not, had anything actually been captured. If, on the other hand, sparsity arises as a result of increasing impacts on an assemblage, to the point where samples become fully azoic, however large the sampler size, then it might be desirable to define those samples as 100% similar (0% dissimilar). Another example is of tracking over time the colonisation of a settlement plate or a rock patch which has been cleared: very sparse assemblages would be inevitable at the start, and one would want to define these early samples as highly similar.
A modified dissimilarity is thus needed, exploiting this extra information that we have from the context, that very sparse samples are to be deemed similar. A simple addition to the denominator of Bray-Curtis achieves this, giving the zero-adjusted Bray-Curtis:
$$ \delta _ {jk} = 100 \left[ \frac{ \sum _ {i=1} ^ p | y _ {ij} - y _ {ik} | }{2 + \sum _ {i=1} ^ p ( y _ {ij} + y _ {ik} ) } \right] \tag{16.1} $$
between samples j and k, where {$y _ {ij}$} is the quantity of species i in the jth sample (for i = 1, .., p species). An alternative way of viewing this coefficient is that it is ordinary Bray-Curtis calculated on a data matrix with an added dummy species consisting of one individual in each sample. This cannot change the numerator, since the dummy species adds |1 - 1| for every pair of samples but it adds 1 + 1 to the denominator for each pair, explaining the 2 on the bottom line of (16.1). A pair of samples containing no species must now be 0% dissimilar because they share the same abundance of their only species (the dummy species), and even two samples that have a single individual of different species will no longer be 100% dissimilar but only 50% dissimilar, because of their shared (dummy) species. And Clarke, Somerfield & Chapman (2006) show that if the numbers in the matrix are not vanishingly small then this zero adjustment can make no difference at all to the resulting resemblance structure. Bray-Curtis will operate as previously but it will behave in a particular (and sometimes required) way for highly denuded samples which ‘go to zero’.
The adjustment is in the same spirit as the use of log transforms on species counts: the $\log(y)$ function will behave badly as $y$ goes to zero (it tends to $- \infty$) so we use $\log(1+y)$, which makes no difference if $y$ is not small but ‘feathers in’ the behaviour as $ y \rightarrow 0$. That analogy is useful because it suggests what we should do for abundances which are not counts but biomass or area cover. Then the dummy value would be better taken not as 1 but the smallest non-zero entry in the matrix¶. In fact, here, the Tikus coral cover does have effectively a minimum value of about 1 after the root-transformation is applied, so this is used both for the quantitative data and for a presence/absence analysis.
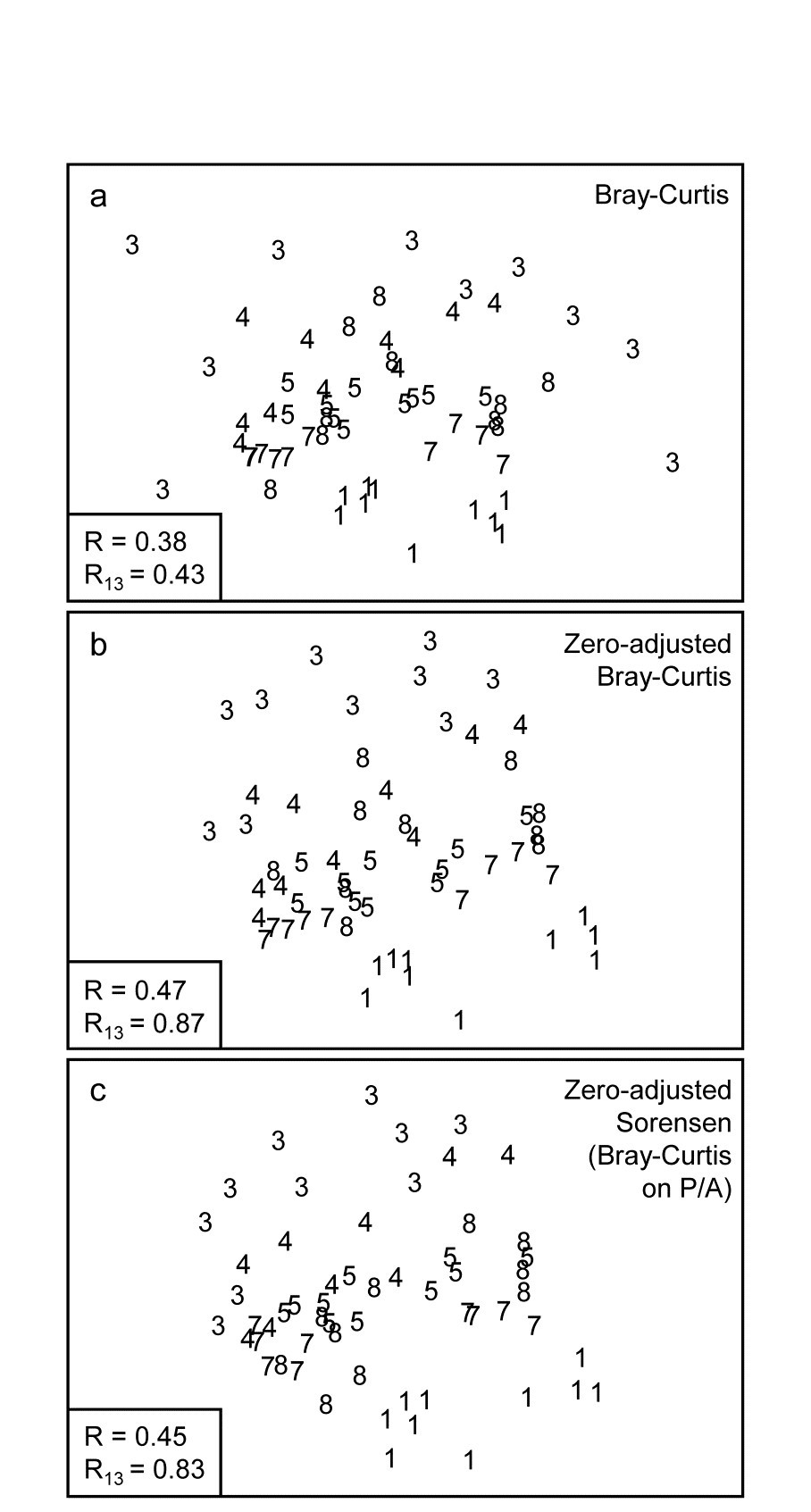
Fig. 16.7. Indonesian reef-corals, Tikus Island {I}. nMDS of 6 years (1=1981, 3=1983, 4=1984, 5=1985, 7=1987, 8=1988), with 10 transects per year. Data are %cover of 75 coral species, $\sqrt{}$-transformed, and similarities calculated as: a) standard Bray-Curtis; b) zero-adjusted Bray-Curtis; c) zero-adjusted Sorensen. The ANOSIM R statistics for the global test (R, among all years) and pairwise (R13, for years 1 and 3 only) are also shown, given that stress values in the MDS are high: a) 0.18; b) 0.21; c) 0.21.
The effect of applying this modification to the Tikus Island corals MDS can be seen in Fig. 16.7a-c, which contrasts the standard Bray-Curtis coefficient with its zero-adjusted form and zero-adjusted Sorensen (eqn. 2.7) which is simply Bray Curtis on species presence/ absence, including an always-present dummy species. The wide spread of 1983 values, which come from a large number of zero similarities within that sparse group, are tightened up substantially with the zero-adjusted coefficient, reflected in the high pairwise ANOSIM statistic $R _ {13} = 0.87$ between 1981 and 1983, cf $R _ {13} = 0.43$ for the standard Bray-Curtis. Sorensen similarly benefits from the use of the adjustment here, since five of the ten 1983 transects have $ \le 2 $ species.
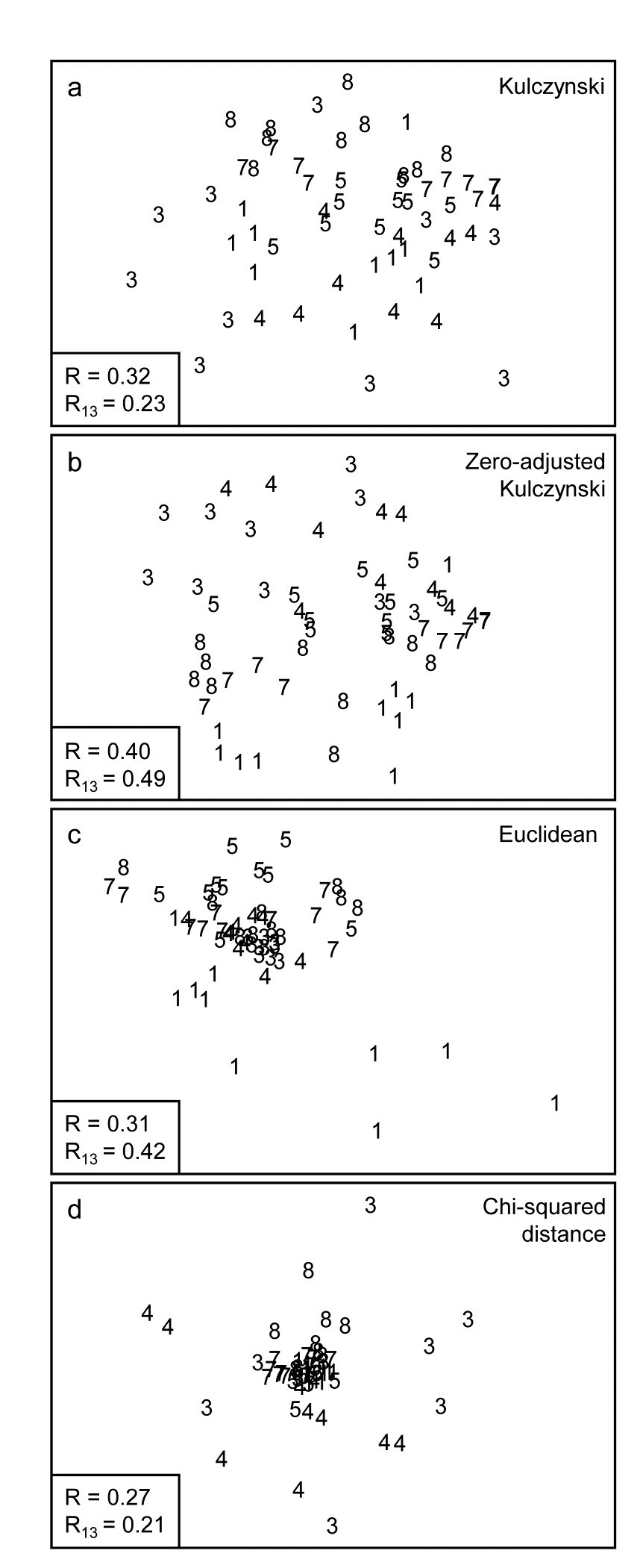
Fig. 16.8. Indonesian reef-corals, Tikus Island {I}. nMDS of 6 years, exactly as in Fig. 16.7, but based on: a) Kulczynski; b) zero-adjusted Kulczynski; c) Euclidean distance; d) $\chi ^ 2$ distance with MDS stress: a) 0.21; b) 0.24; c) 0.12; d) 0.13. Global and pairwise (81 v 83) ANOSIM R statistics again shown.
The Kulczynski similarity (equation 2.4), Fig. 16.8a, is also in the Bray-Curtis family and, whilst it would appear to perform less satisfactorily than Bray-Curtis in this case, and also generally (though see Faith, Minchin & Belbin (1987) and footnote on page 2.2), it too benefits from the dummy species adjustment, Fig. 16.8b. Even more dramatic changes are seen to these plots for a wider range of coefficients: Euclidean distance (eqn 2.13, Fig. 16.8c) reverses the within-group dispersion of 1981 and 1983 samples. All these analyses (apart from P/A measures) are on square-root transformed area cover, but even after transformation there are big differences in total cover between the samples, and Euclidean distance is primarily dominated by these, with the tight cluster of 1983 transects resulting from the strong reduction in total cover noted earlier.
The $\chi ^ 2$ distance measure, defined as:
$$ d _ {jk} = \sqrt{ \sum _ i \frac{1}{y _ {i+} / \sum _ i y _ {i+}} \left[ \frac{y _ {ij} }{ \sum _ i y _ {ij}} - \frac{y _ {ik} }{ \sum _ i y _ {ik}} \right] ^ 2} $$
$$ y _ {i+} = \sum _ j y _ {ij} \tag{16.2} $$
which is the implicit dissimilarity in Correspondence Analysis (CA) and its detrended (DCA) and canonical versions (CCA), is seen to be at the other end of the spectrum (Fig. 16.8d), increasing the spread of 1983 (and 1984) values further than standard Bray-Curtis and collapsing the 1981 transects almost to a single point. The $\chi ^ 2$ distance coefficient is always susceptible to dominance by rare species, with very small area covers, since its genesis is for data values which are real frequencies†. The problem can be seen in the (first) denominator for each term in the sum, which is the total across samples for each species, an area cover which can be very small, giving instability. (In fact three outlying 1983 replicates are omitted in Fig. 16.8d to even get this plot). Another implication of the form of this coefficient is that methods based on CA always standardise samples (the denominators inside the squared term are totals across species for each sample) hence the effects of much larger total (square-rooted) area covers in 1981, which dominate the Euclidean plot, entirely disappear for $\chi ^ 2$ distance. The Bray-Curtis family coefficients are intermediate in this spectrum: they make some use of differences in sample totals but are also influenced by the species presence/absence structure, a feature with no special role in Euclidean (and similar) distance measures.
Other quite commonly used coefficients§ (for which MDS ordinations are not shown) include Manhattan distance, equation (2.14), whose behaviour is close to that of Euclidean distance though it should be less susceptible to outliers in the data, because distances are not squared as in the Euclidean definition. Note that Manhattan does, however, share some affinity of definition with Bray-Curtis. To within a constant, Bray-Curtis will reduce to Manhattan distance when the totals of all (transformed) data values for samples, summed across species, are the same. For the data of Fig. 16.8, the Manhattan ordination is very similar to that for the Euclidean plot (Fig. 16.8c); it gives global $R = 0.28$ and pairwise $R _ {13} = 0.38$.
The normalised form of Euclidean distance, in which each species is first centred at its mean over samples (again after transformation) and, more importantly, divided by its standard deviation over samples, is about as inappropriate a measure for species data as could be envisaged! This is both because it does not honour the status of a zero entry as indicating species absence (as noted on page 2.4, the zeros are replaced by a different number for each species) and also because each species is now given exactly the same weight in the calculation, irrespective of whether it is very rare or extremely common, often a recipe for anarchy in the ensuing analysis. And indeed the MDS plot for the coral data is essentially a slightly more extreme form of the Euclidean plot of Fig. 16.8c, with even lower ANOSIM statistics of $R = 0.19$, $R _ {13} = 0.34$. It should be noted, of course, that normalised Euclidean is a perfectly sensible resemblance measure (usually the preferred choice) for data of environmental type, in which zeros play no special role and the variables are on different measurement scales, hence must be adjusted to a common scale.
The basic form of Gower’s coefficient ( Gower (1971) ) is defined as:
$$ d _ {jk} = \frac{1}{p} \sum _ i \frac{ | y _ {ij} - y _ {ik} | }{ R _ i} \tag{16.3} $$
where the Manhattan-like numerator is standardised by dividing by the range for that species across all samples, $ R _ i = \max _ i \left[ y _ {ij} \right] - \min _ i \left[ y _ {ij} \right] $ . Since nearly all species will often be absent somewhere in the set of samples, in effect this is calculating Manhattan on a data matrix which has been species-standardised by the species maximum‡. The equal weight it therefore gives to each species and the use of a simple distance measure on those standardised values ensures that it will behave very similarly to normalised Euclidean, as is observed for the coral MDS plot; global $R$ is 0.21 and $ R _ {13} = 0.39$. There is, however, a form of the Gower measure in which joint absences are identified and removed from the calculation. In practice this just means that the p divisor (the number of species in the matrix) outside the sum in (16.3) is replaced by the number of non-jointly absent species for each specific pair of samples. The same trick was seen in (2.12) in the
Stephenson, Williams & Cook (1972)
formulation of Canberra similarity, and it has a major effect in bringing both coefficients into step with one of the defining guidelines of biologically-useful measures, viz. point (d) on page 2.3, that jointly absent species carry no information about similarity of those two samples. The MDS plot for the Gower (exc 0-0) coefficient does result in a configuration closer to that for the (zero-adjusted) Bray-Curtis than it is to the basic Gower coefficient and gives
$R = 0.41$, $R _ {13} = 0.61$. The Canberra measure here gives highly similar plots and ANOSIM values to Bray-Curtis (as is quite often the case, since it does satisfy all the ‘Bray-Curtis family’ guidelines, page 2.2), and also benefits in the same way from adding the ‘dummy species’, giving $R = 0.48$, $R _ {13} = 0.87$.
Second-stage MDS on resemblance measures
This plethora of MDS plots and, more importantly, the relationships among their underlying resemblance matrices, can best be summarised using the same tool as for comparing different transforms or taxonomic levels, earlier in this section: the second stage MDS. This is based on similarities of similarity coefficients typically measured by the usual (RELATE) Spearman rank correlations between every pair of resemblance matrices, which values are themselves re-ranked as part of the second-stage nMDS ordination⸙.
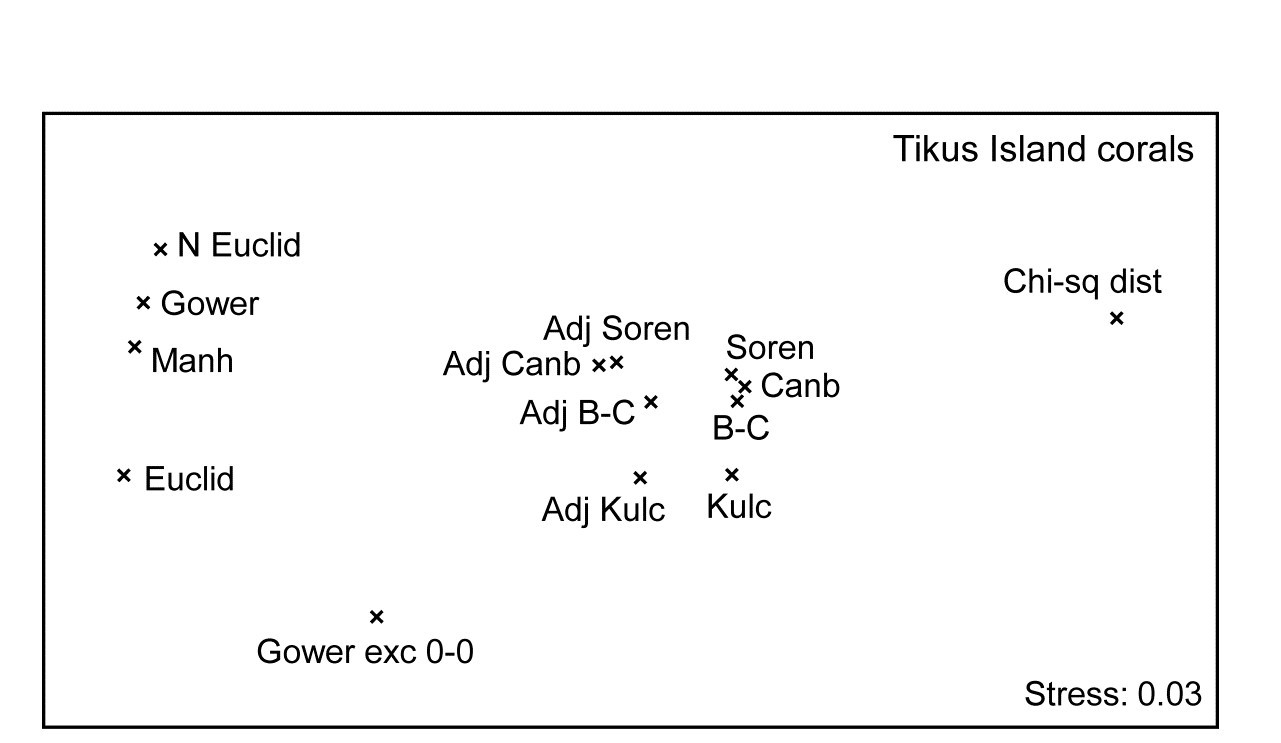
Fig. 16.9. Indonesian reef-corals, Tikus Island {I}. Second-stage MDS of Spearman matrix correlations between every pair of 14 resemblance matrices, calculated from square-root cover from 75 species on 60 reef transects. (The ‘fix collapse’ option, on page 5.8, was applied in this case℈). Resemblance coefficients are: Euclidean (normalised or not), Gower (excluding joint absences or not), Manhattan, $\chi ^ 2$ distance, and four ‘biological’ measures, all calculated with zero-adjustments (dummy species) or not: Bray-Curtis, Kulczynski, Canberra and Sorensen (the latter on presence/absence data). Proximity of coefficients indicates how similarly they describe multivariate patterns of the 60 samples.
Fig. 16.9 displays the second-stage nMDS plot for 14 resemblance measures, calculated on the Tikus Island samples, for some of which measures the (first-stage) MDS plots are seen in Figs. 16.7 & 16.8. Such second stage plots, of relationships amongst the multivariate patterns obtained by different coefficient definitions, tend to display a consistent pattern for different data sets. As with the discussion on Fig. 8.16, on patterns of correlation between differing diversity definitions, what such plots are able to reveal is not primarily the characteristics of particular data sets, but mechanistic relationships among the indices/coefficients. These arise as a result of their mathematical form, and the way that form dictates which general features of the data are emphasised and what assumptions they make (implicitly) about issues such as those listed on page 2.2): should the result be a function of sample totals?; are all the species to be given essentially similar weight?; are joint absences to be ignored?; should the coefficient have a concept of complete dissimilarity?; etc.
It is evident from the figure that the ‘biological’ coefficients do take a strongly similar view of the data and that the zero-adjustment does affect the outcome in the same way for all four such measures. Interestingly the difference between square-root transformed and presence/absence data under the same Bray-Curtis coefficient (the Sorensen point is Bray-Curtis on P/A) is hardly detectable amongst the major differences seen in changing to a different coefficient. The move from Euclidean to normalised Euclidean, and similar coefficients giving species equal weight irrespective of their total/range, is also very evident (this sequence of coefficients on the extreme left of the plot is also consistent across data sets), and the very different view taken of this data by the $\chi ^ 2$ distance measure is equally clear. Taken together, this plot is a salutary lesson in the importance of choosing an appropriate similarity measure for the scientific context, and making consistent use of it for all the analyses of that data setȹ.
Other data sets will produce similar patterns to Fig. 16.9, though with subtle and interesting differences, e.g. if sparsity of samples is not an issue then the zero-adjusted coefficients will be totally coincident with their standard forms. For data in which turnover of species under the different conditions (sites/times/ treatments) is low, then coefficient differences will generally have smaller effect℈ - thankfully not all data sets produce the distressingly large array of outcomes seen in Figs 16.7 and 16.8!
Clarke, Somerfield & Chapman (2006)
give a number of further examples, but we shall show one more instructive example, that of the Clyde macrobenthic data first seen in Chapter 1, Fig. 1.11.
Garroch Head macrofauna counts
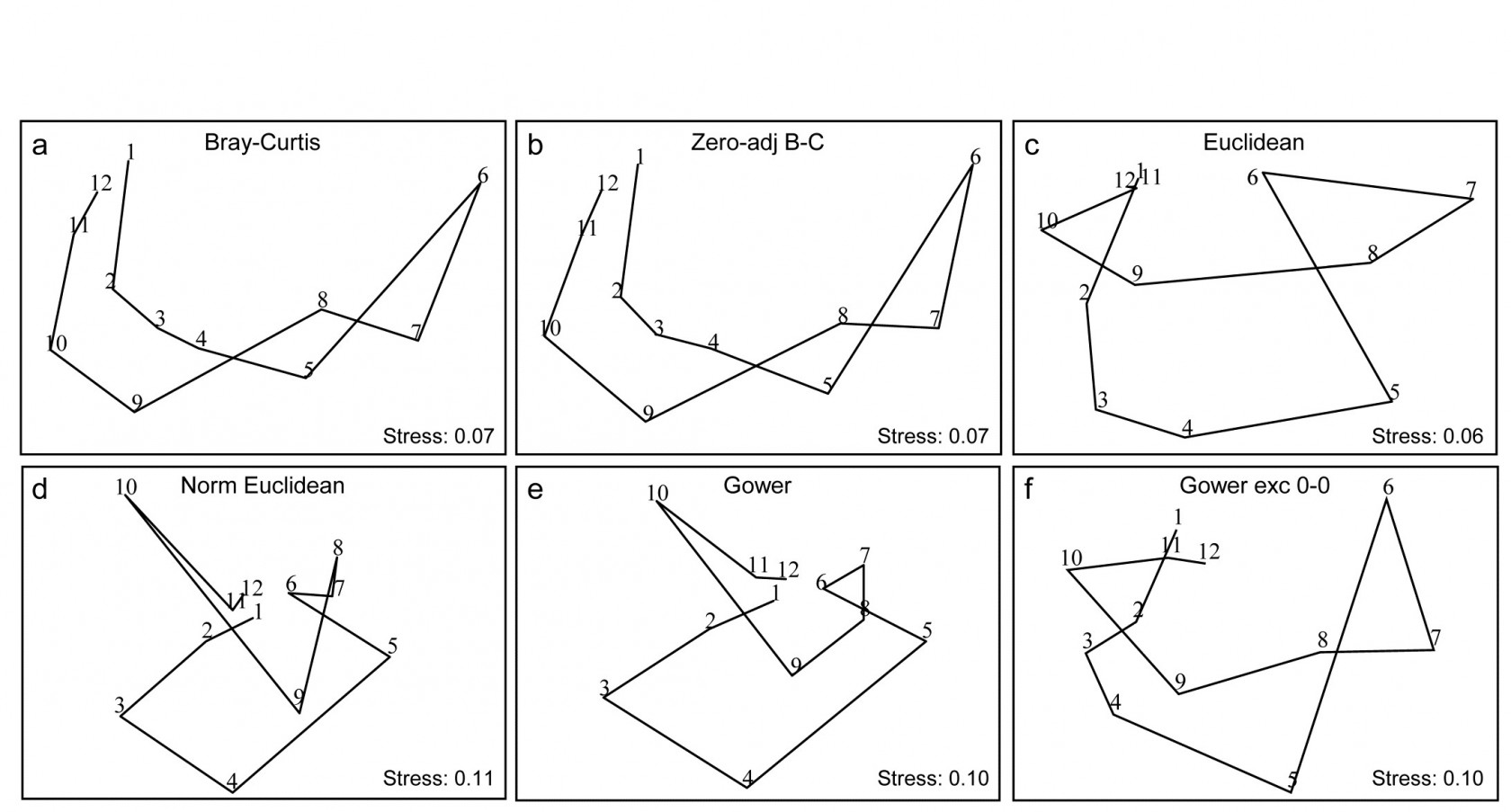
Fig. 16.10. Garroch Head macrofauna {G}. 2-d nMDS of counts of 84 species from soft-sediment benthic samples along a transect of 12 sites (1-12) in the Firth of Clyde (see map fig. 8.3), across the sludge disposal location (site 6). Counts are fourth-root transformed with resemblance measures: a) standard Bray-Curtis (equation 2.1), b) zero-adjusted Bray-Curtis (16.1), c) Euclidean distance (2.13), d) normalised Euclidean distance (p4-6), e) basic Gower coefficient (16.3), f) Gower excluding joint absences (p16-10).
Previous analyses of the E-W transect of 12 sites over the sewage-sludge dumpground in the Firth of Clyde, {G}, have been of the macrofaunal biomass data (e.g. Figs. 1.11, 7.9, 11.5) but Fig. 16.10 is of fourth-root transformed counts for the 84 macrobenthic species, ordinated using six different resemblance measures. The main feature of this data is the steady change in community as the dump centre (site 6) is approached and steady reversion back to a similar community at the opposite ends of the transect (sites 1 and 12). As the ‘meta-analysis’ of Fig. 15.1 shows, this is a major change in assemblage resulting from a clear pattern of impact of organic enrichment and (most) heavy metal concentrations on nearing the dump centre, Fig. 11.1. In fact, only three species are found at site 6, though in reasonably large numbers (76 Tubificoides benedii, 4 Capitella capitata and 250 nematodes, meiofauna which were not taxonomically separated in this study but captured in a macrofauna sieve by virtue of their large size). These species are virtually absent from sites 1, 2, 11 and 12, which are characterised by a distinctly different suite of species (e.g. Nuculoma, Nucula, Spiophanes sp.) but still with rather modest total counts (<200 individuals at any of those 5 sites). At in-between sites along the transect, the number of species and the total number of individuals steadily increase then decrease, as the dump centre is neared. This appears a classic case of the intermediate disturbance hypothesis ( Connell (1978) ; Huston (1979) ), as a result of the organic enrichment, in which the richness diversity and abundance increase with mild forms of disturbance, because of influx of opportunist species (typically small-bodied and in large numbers) before everything crashes at severe impact levels. Such a clear and ecologically meaningful pattern is quite enough to completely confuse some distance measures in Fig. 16.10! Euclidean distance (whether normalised or not) and the basic form of the Gower coefficient are strongly influenced by the fact that the abundance totals are similar at the ends and mid-point of the transect, and the fact that these sites have many jointly-absent species, i.e. joint absences are inferred as evidence for similarity of samples, whereas they are nothing of the sort. The species which are present are largely completely different ones, which will indicate some dissimilarity in all coefficients, but this contribution is largely overwhelmed by the evidence for similarity from joint absences in the inappropriate distance measures! The net effect is for the latter ordinations to show sites 6 and 7 merging with 1, 11 and 12 in a highly misleading way. The Bray-Curtis family, on the other hand - and to a lesser extent, the Gower coefficient, excluding joint absences - have no problem generating the correct and meaningful ecological gradient here, though the latter’s insistence on giving the rare species equal weight with dominant ones does tend to diffuse the tight gradient of change. Note also (Fig. 6.10a & b) that no useful purpose is served by a ‘dummy species’ addition: none of the samples is sparse enough for the zero-adjusted coefficients to alter the relative among-sample similarities.
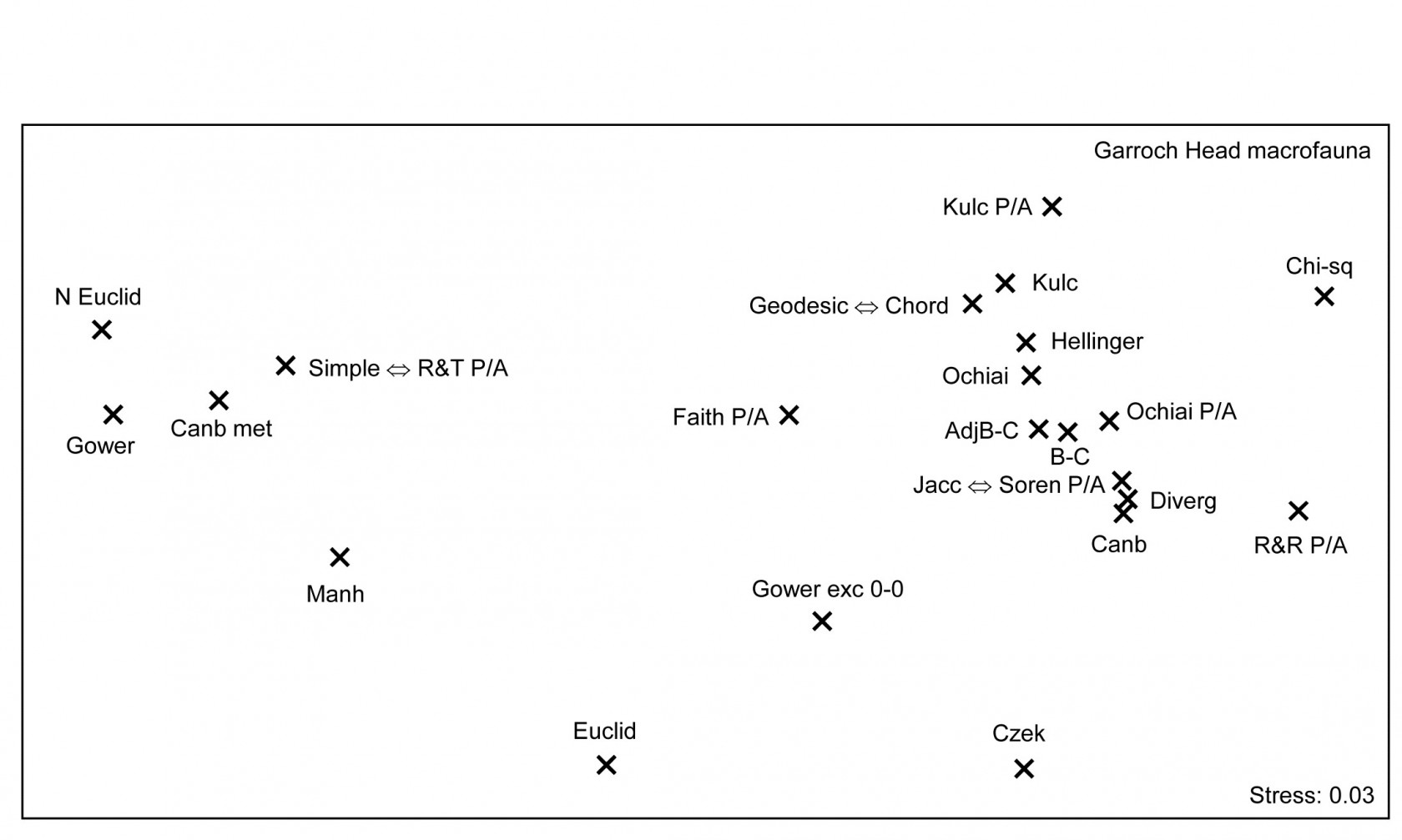
Fig. 16.11. Garroch Head macrofauna {G}. Second-stage MDS of Spearman matrix correlations between every pair of 25 resemblance matrices, calculated from fourth-root counts of 84 species on a transect of 12 sites across the sludge disposal site. Resemblance coefficients are: Euclidean (normalised or not), Gower (exclude joint absences or not), Manhattan, Hellinger and chi-squared distance, the coefficient of divergence, Canberra similarity and Canberra metric, Bray-Curtis (zero-adjusted or not), Kulczynski (and in P/A form), Ochiai (and in P/A form), Czekanowski’s mean character difference, Faith P/A, Russell & Rao P/A, and three pairs of coefficients which are coincident since they are monotonically related to each other (denoted by $\Leftrightarrow$): Simple matching and Rogers & Tanimoto P/A, Geodesic metric and Orloci’s Chord distance, and finally Jaccard and Sorensen P/A (the P/A form of Bray-Curtis). See the PRIMER User manual for definition of all coefficients.
Fig. 6.11 is the second-stage MDS from the Spearman matrix correlation ($\rho$) among a very wide range of coefficients, not all of which have been defined here but all of which are available on the PRIMER menu for resemblance calculation (and for which equations are given in the User Manual). They exclude those coefficients which are designed for untransformed, real counts, with coefficients constructed from multinomial likelihoods, and other measures with their own built in transformations (e.g. ‘modified Gower’) which cannot then sensibly be applied to fourth-root transformed data. All the displayed measures are thus compared on the same (transformed) data though note that several of the coefficients utilise only presence or absence data. Only one zero-adjusted similarity - that for Bray-Curtis - is included, since the adjustment is rather minor in all cases for this example.
Similar groupings are evident as for the previous Fig. 6.9, for those coefficients which are present in both, though a number of measures which are only in Fig. 6.11 are seen to take further different ‘views’ of the data. (Note that the wider range of inter-relationships ensured that the nMDS did not collapse as previously and there was no need to stabilise the plot by mixing with a degree of metric stress). Note again the large difference made by adjusting for joint absences, both between the forms of the Gower coefficient, as seen previously (the scale of this change can be seen in Fig. 16.10e & f), and the equivalent difference for the Canberra similarity of equation (2.12), as used in Fig. 16.9, and the Canberra metric which is a function of joint absences. Three pairs of coefficients identified in the legend to Fig. 16.11 do not have precisely the same mathematical form but it is straightforward to show that they increase and decrease in step (though not linearly), i.e. their ranks similarities/distances will be identical. The best known of these are the two presence/absence measures, Sorensen and Jaccard, which because of this monotonic relation will give identical nMDS plots, ANOSIM tests etc for all data sets (though not identical PERMANOVA tests). Note also that, though the differences between fourth-root transform and P/A for the same measure (Bray-Curtis to Sorensen, Ochiai, Kulczynski) are not large, they are consistent and non-negligible, indicating that the data have not been over-transformed to a point where all the quantitative information is ‘squeezed out’. Bray-Curtis, Ochiai and Kulczynski are also seen to fall in logical order (of the arithmetic, geometric and harmonic means in their respective denominators).
Many such subtle points to do with construction of coefficients can be seen in the second-stage plots, but another strength is their ability to place in context any proposed measure, perhaps newly defined (and the ease with which plausible new coefficients can be defined was commented on in the footnote on page 2.2)). If a new measure is an asymptotic equivalent of an existing one, the two points will be consistently juxtaposed; if it captures new aspects of similarity or distance, it should occupy a different space in the plot. Together with assessments of the theoretical rationale or mathematical form of coefficients, the practical implications seen from a second-stage plot might therefore help to provide a way forward in defining a classification of resemblance measures.
¶ The PRIMER Resemblance routine offers addition of a dummy species, with a specified dummy value, for any coefficient, since the idea will apply to other members of the Bray-Curtis family (page 2.2)), but it will not always make sense, and on coefficients not excluding joint absences (such as distance measures) it will have little or no effect at all. As with the log transform, choice of the dummy value is a balance between being too small to be relevant (it will always give two blank samples a similarity of 100% but two nearly blank samples can still be effectively 0% similar) or too large and thus impact on samples that are not at all denuded.
† The theoretical basis of CA is that the entries in the matrix are real frequencies, following multinomial distributions for each species (the distributional basis of $\chi ^2$ tests, for example), which this distance measure reflects. Species count matrices are never real frequencies because individuals are not distributed randomly (and with the same mean density) over the area or water volume being sampled, i.e. they are clumped, not Poisson distributed (see page 9.5). Real frequencies are produced from, say, several quadrats taken for each sample, which are then condensed to ‘number of quadrats in which species X is found’. Where such sampling is possible, frequency data can be an effective alternative to strong transformation or dispersion weighting of highly clumped counts, or of dominance of area cover % by a few large and common rocky shore algae or coral species, see for example Clarke, Tweedley & Valesini (2014) . Even for such data, a $\chi ^2$ distance measure can still be problematic in respect of the rare species (the mantra for $\chi ^2$ tests in standard statistics, that ‘expected frequencies should be >5’, arises for much the same reason) and the CA-based methods in the excellent CANOCO package ( ter Braak & Smilauer (2002) ) build in a downweighting of rare species to circumvent the issue.
§ PRIMER offers about 45 different resemblance measures, under (not mutually exclusive) divisions of: similarity or dissimilarity/ distance; quantitative or P/A; correlation; and the P/A taxonomic dissimilarity measures at the end of Chapter 17.
‡ Standardising species (or samples) either by their totals or by their maxima, are options offered by the PRIMER Standardise routine, under the Pre-treatment menu.
⸙ There is little necessity to worry about whether these Spearman matrix correlations are all positive, as befits similarities. Indeed some are not, such is the disagreement between Fig. 16.8c & d for example, giving RELATE $\rho = -0.22$! Positivity can be ensured by the conversion $S = 50( 1 + \rho )$, but this is unnecessary if nMDS is to be used, because only the rank orders of the values matter.
ȹ It is one if the authors’ bête noires to see how inconsistent and incompatible a use some ecologists make of the available multivariate tools. The Cornell Ecology routines (detrended CA, and TWINSPAN) and CANOCO’s CA and CCA plots and tests (from $\chi ^2$ distance), classic PCA, canonical correlation, MANOVA or discriminant analysis (from Euclidean or Mahalanobis distance), PRIMER and PERMANOVA+ methods such as MDS, ANOSIM, SIMPER, PERMANOVA etc (using a specific measure such as Bray-Curtis) all have their place in historical development and current use, but it is generally a mistake to mix their use across different implicit or explicit resemblance measures on the same data matrix. (Of course different data matrices, e.g. for species or environmental variables, will usually need different coefficient choices). Choice of coefficient (and to a lesser extent transformation) is sufficiently important to the outcome, that you need: a) to understand why you are choosing this particular coefficient and transformation, b) to apply it as consistently as possible to your testing, visualisation and interpretation of that matrix.
℈ The differences between coefficients are so stark for the Tikus Island data that the nMDS shown by Clarke, Somerfield & Chapman (2006) did collapse into three groups: Euclidean to Normalised Euclidean, the ‘biological’ measures and $\chi ^2$ distance (all correlations among those three groups being smaller than any correlations within them), and two of the groups were separately ordinated. Here Fig. 16.9 can avoid this problem by using PRIMER v7’s new ‘fix collapse’ option, page 5.8, in which a small amount (5%) of mMDS stress is mixed with 95% nMDS stress, to stabilise the plot.