6.7 Example: Eaglehawk Neck meiofauna (two-way crossed case)

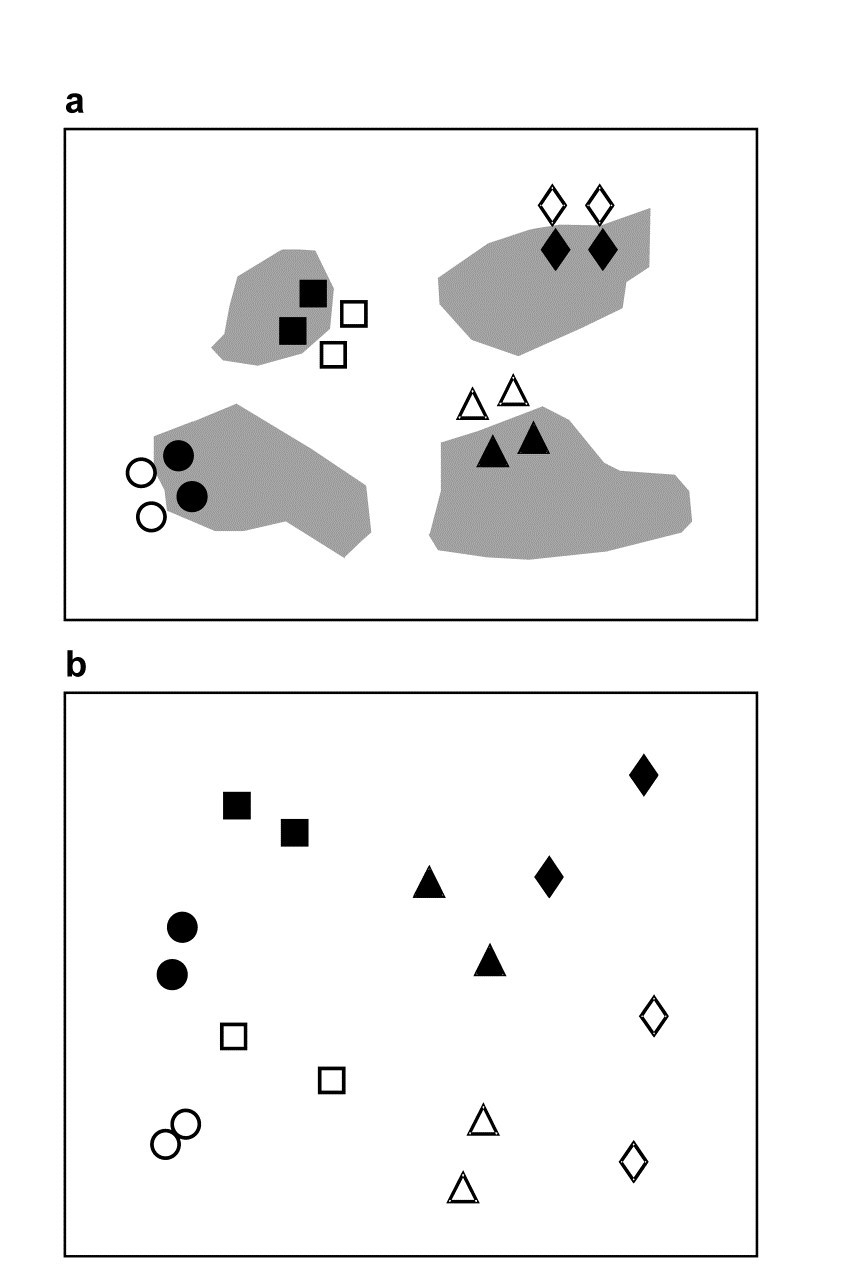
An example of a two-way crossed design is given in Warwick, Clarke & Gee (1990) and is introduced more fully here in Chapter 12. This is a so-called natural experiment, studying disturbance effects on meiobenthic communities by the continual reworking of sediment by soldier crabs. Two replicate samples were taken from each of four disturbed patches of sediment, and from adjacent undisturbed areas, on a sand flat at Eaglehawk Neck, Tasmania; Fig. 6.7a is a schematic representation of the 16 sample locations. There are two factors: the presence or absence of disturbance by the crabs and the ‘block effect’ of the four different disturbance patches. It might be anticipated that the community will change naturally across the sand flat, from block to block, and it is important to be able to separate this effect from any changes associated with the disturbance itself. There are parallels here with impact studies in which pollutants affect sections of several bays, so that matched control and polluted conditions can be compared against a background of changing community pattern across a wide spatial scale. There are presumed to be replicate samples from each treatment/block combination (the meaning of the term crossed), though balanced numbers are not essential.

For the Eaglehawk Neck data, Fig. 6.7b displays the MDS for the 16 samples (2 treatments $\times$ 4 blocks $\times$ 2 replicates), based on Bray-Curtis similarities from root-transformed abundances of 59 meiofaunal species. The pattern is remarkably clear and a classic analogue of what, in univariate two-way ANOVA, would be called an additive model. The meiobenthic community is seen to change from area to area across the sand flat but also appears to differ consistently between disturbed and undisturbed conditions. A test for the latter sets up a null hypothesis that there are no disturbance effects, allowing for the fact that there may be block effects, and the procedure is then exactly that of the 2-way ANOSIM test for hypothesis H1 of the nested case. For each separate block an R statistic is calculated from equation (6.1), as if for a simple one-way test for a disturbance effect, and the resulting values averaged to give $\overline{R}$. Its permutation distribution under the null hypothesis is generated by examining all simultaneous re-orderings of the four labels (two disturbed, two undisturbed) within each block. There are only three distinct permutations in each block, giving a total of $3^4$ (= 81) combinations overall and the observed value of $\overline{R}$ (= 0.94) is the highest value attained in the 81 permutations. The null hypothesis is therefore rejected at a significance level of just over 1%.

Fig. 6.7. Tasmania, Eaglehawk Neck {T}. a) Schematic of the ‘2-way crossed’ sampling design for 16 meiofaunal cores with two disturbed and two undisturbed replicates from each of four patches of burrowing activity by soldier crabs (shaded). b) MDS of species abundances for the 16 samples, showing separation of the blocks on the x-axis and discrimination of disturbed from undisturbed communities on the y-axis (stress = 0.11).
 

The procedure departs from the nested case because of the symmetry in the crossed design. One can now test the null hypothesis that there are no block effects, allowing for the fact that there are treatment (disturbance) differences, by simply reversing the roles of treatments and blocks. $\overline{R}$ is now an average of two R statistics, separately calculated for disturbed and undisturbed samples, and there are $8!/[(2!)^4 4!] = 105$ permutations of the 8 labels for each treatment. A random selection from the $105^2 = 11,025$ possible combinations must therefore be made. In 1000 trials the true value of $\overline{R}$ (=0.85) is again the most extreme and is almost certainly the largest in the full set; the null hypothesis is decisively rejected. In this case the test is inherently uninteresting but in other situations (e.g. a sites $\times$ times study) tests for both factors could be of practical importance.