6.12 Two-way ordered ANOSIM designs
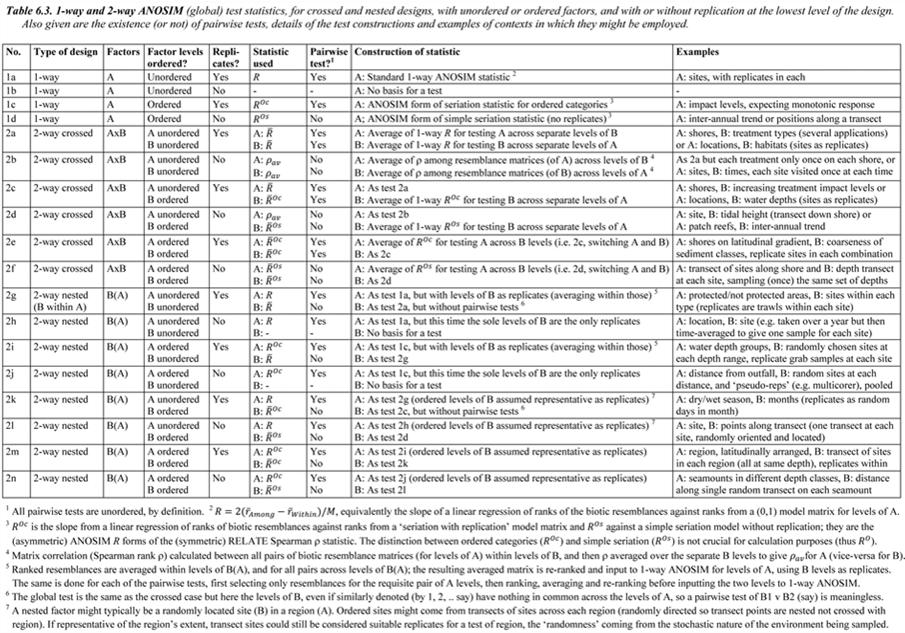
Under the non-parametric framework adopted in this manual (and in the PRIMER package) three forms of 2-way ANOSIM tests were presented on page 6.5: 2-factor nested, B within A (denoted by B(A)); 2-factor crossed (denoted A$\times$B); and a special case of A$\times$B in which there are no replicates, either because only one sample was taken for each combination of A and B, or replicates were taken but considered to be ‘pseudo-replicates’ (sensu Hurlbert (1984) ) and averaged.¶
The principle of these tests, and their permutation procedures, remain largely unchanged when A or B (or both factors) are ordered. Previously, the test for B under the nested B(A) model (page 6.6) averaged the 1-way $R$ statistic for each level of A, denoted $\overline{R}$, and the same form of averaged statistic was used for testing B under the crossed A$\times$B model with replicates (page 6.7); without replicates the crossed test used the special (and less powerful) construction of page 6.8, with test statistic the pairwise averaged matrix correlation, $\rho_{av}$. (There was no test for B in the nested model, in the absence of replicates for B). If B is now ordered, $R$ is replaced by $R^{Oc}$ where there are replicates (becoming $\overline{R}^{Oc}$ when averaged across the levels of A), or by $R^{Os}$ where there are not (becoming $\overline{R}^{Os}$); there is no longer any necessity to invoke the special form of test based on $\rho_{av}$ when the factor is ordered. The same substitutions then happen for the test of A, if it too is ordered: $\overline{R}$ and $\rho_{av}$ are replaced by $\overline{R}^{Oc}$ and $\overline{R}^{Os}$. If A is not ordered, any ordering in B does not change the way the tests for A are carried out, e.g. for A$\times$B, the A test is still constructed by calculating the appropriate 1-way statistic for A, separately for each level of B, and then averaging those statistics.
Such a plethora of possibilities are best summarised in a table, and the later Table 6.3 lists all the possible combinations of 2-way design, factor ordering (or not) and presence (or absence) of replicates, giving the test statistic and its method of construction, listing whether or not pairwise tests make sense†, and then giving some examples of marine studies in which the factors would have the right structure for such a test.
We have already seen unordered examples of 1-way tests (1a, Table 6.3) in Figs. 6.3 & 6.5, 2-way crossed (2a) in Fig. 6.7 and, without replication (2b), in Figs. 6.10 & 6.12; Fig. 6.6 is 2-way nested (2g). Examples of 2-way crossed without replicates, with one (2d) or both (2f) factors ordered, now follow.
¶ An example of the latter might be ‘replicate’ cores from a multi-corer deployed only once at each of a number of sites (A) for the same set of months (B); these multiple cores are neither spatially representative of the extent of a site (a return trip would result in multi-cores from a slightly different area within the site) nor, it might be argued, temporally representative of that month.
† If they do make sense, the PRIMER7 ANOSIM routine will give them. Performing such a 2-(or 3-) way analysis is much simpler than reading these tables! It is simply a matter of selecting the form of design (all likely combinations of 1-, 2- or 3-factor, crossed or nested) and then specifying which factors are to be considered ordered – the factor levels must be numeric in that case but only their rank order is used. Analyses that use specific numerical levels (unequally-spaced) can be catered for in many cases within the expanded RELATE routine, utilising a $\rho$ statistic, see Chapter 15.