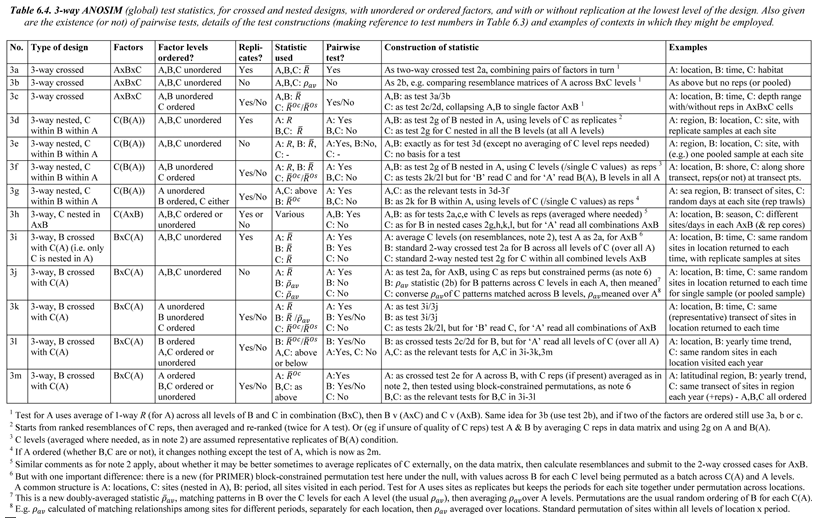
6.14 Three-way ANOSIM designs

Table 6.4 details all viable combinations of 3 factors, A, B, C, in crossed/nested form, ordered/unordered, and with/without replication at the lowest level. Fully crossed designs are denoted A$\times$B$\times$C, e.g. locations (A) each examined at the same set of times (B) and for the same set of depths (C) ^¶.
 

 

With a fully symmetric design like this (cases 3a-c in Table 6.4), the idea is to test each factor in turn (A, say), by ‘flattening/collapsing’ the other two into a single factor (B$\times$C) whose levels are all the possible combinations of levels of B and C; the test for A from the relevant 2-way crossed design is then carried out. E.g. the global test for time effects (B removing A$\times$C) will only compare those different times at the same depth and location, and will then average those time-comparison statistics across all depth by location levels. Whichever of the definitions $\overline{R}$ / $\overline{R}^{Oc}$ / $\overline{R}^{Os}$ / $\rho_{av}$ is used, the three global statistics (A removing B$\times$C, B removing A$\times$C, C removing A$\times$B) can be directly compared to gauge relative importance of A, B & C.

The fully nested design C(B(A)), e.g. area (C) nested in site (B), nested in location (A), cases 3d-g, can also be handled by repeated application of the 2-way case. This tests the lowest factor (C) inside the levels of the next highest (B), then averaging (in some form, see later) the replicate level, so that levels of C are now replicates for a test of B, then averaging the levels of C so that B levels are the replicates for a test of A.

Another straightforward possibility is C(A$\times$B), 3h, in which C is nested in all combinations of A and B, e.g. multiple sites (C) are chosen from all combinations of location (A) and habitat type (B), in a case where all habitat types are found at each location, with replication (or not) at each site. The test for C uses the A$\times$B ‘flattened’ factor at the top level of a 2-way nested design, and tests for A and B are exactly as for the 2-way crossed design but, if replicates exist, averaging them (again, in some form) to utilise the levels of C as replicates for the crossed A and B tests.

The only other practical combination, and one which is quite frequently encountered, is B$\times$C(A), 3i-m, in which only C is nested in A, and B is crossed with C, e.g. multiple sites (C) are identified at locations (A), and the same sites are returned to in each of a number of seasons (B), with (or without) genuine replicate day/area samples taken at each site in each season. Here there are one or two new issues of principle and these are illustrated in more detail later.

^¶ One of the commonest mistakes made by people new to ANOVA-type designs (whether in ANOSIM or PERMANOVA) is to assume here that depth is a nested factor in location, since the differing depth samples are all taken at the same location. But they are the same depths (or depth ranges) across locations, hence one can remove the location effect when studying depth and the depth effect when studying location, which is the whole point and power of a crossed design.