9.6 Example: Fal estuary copepods

Somerfield, Gee & Warwick (1994a) and Somerfield, Gee & Warwick (1994b) present biotic and environmental data from five creeks of the Fal estuary, SW England, whose sediments can contain high heavy metal levels resulting from historic tin and copper mining in the surrounding valleys ({f}, Fig. 9.3).

Fig. 9.3 Fal estuary copepods {f}. Five creeks sampled for meiofauna/macrofauna
 

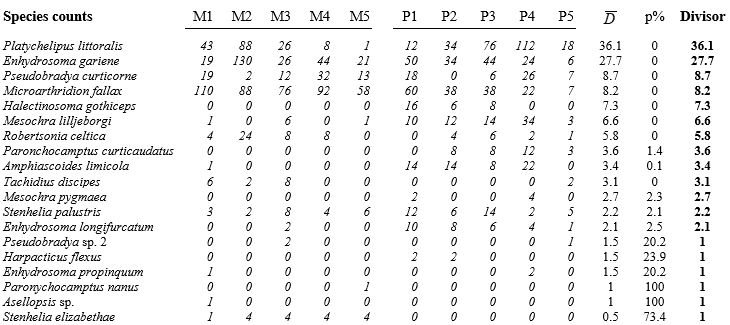
Table 9.6. Fal estuary copepods {f}. Original counts from five replicate meiofaunal cores in each of two creeks (Mylor and Pill). Final three columns give the average dispersion index, its significance, and the divisor used to downweight each row (matrix is ordered by the latter) under the dispersion weighting procedure. Divisor=1 if permutation test does not give significant clumping for that species.

 

Here, only the infaunal copepod counts are analysed, from five replicate meiofaunal cores in each of two creeks (Mylor, M and Pill, P), subject to differing sediment concentrations of contaminants (Table 9.6). Species are listed in decreasing order of their average dispersion index $\overline{D}$ over the two groups, e.g. for the first species, Platychelipus littoralis, $D _ M =35.9$ and $D _ P =36.2$, giving average $\overline{D} = 36.1 $, the divisor for the first row of the matrix. This represents rather strong overdispersion for this species, as does the divisor $\overline{D} = 27.7$ for the second row, Enhydrosoma gariene. In fact, the highest counts in the matrix are found in these two species and, without DW, they would have played an influential role in determining the similarity measures input to the multivariate analyses. But their counts are not consistent over replicates, ranging from 1 to 88, 12 to 112, 19 to 130 etc, hence giving large dispersion indices (variance-to-mean ratios). The dispersion-weighted values, however, are now much lower, ranging only up to 3 or 4, and therefore strongly down-weighted in favour of more consistent species (over replicates), such as Microarthridion fallax. Its counts were initially similarly high but are subject to a much lower divisor, so this fourth row of the weighted matrix now ranges up to 13, giving it much greater prominence. Interestingly, even quite low-abundance species, such as the last in the list (Stenhelia elizabethae) will now make a significant contribution, because of its consistency; it does not get down-weighted at all, as the following permutation test shows.
 

Test for overdispersion

The final six species in the table exhibit no significant evidence of overdispersion at all, and their divisor is therefore 1. What is needed here to examine this is a test of the null hypothesis $D=1$ in all groups, and a relevant large-sample test is based on the standard Wald statistic for multinomial likelihoods (further details in Clarke, Chapman, Somerfield et al. (2006) ). This has the familiar chi-squared form, e.g. for Tachidius discipes how likely is it that observed counts for Mylor of 6, 2, 8, 0, 0 could arise from placing 16 individuals into 5 replicates independently and with equal probability, i.e. when the ‘expected’ values in each replicate are 3.2? Simultaneously, how likely is it that the two individuals from Pill both fall into the same replicate if they arrive independently (i.e. observed values are 0, 0, 0, 0, 2 and expected values 0.4 in each cell)? The usual chi-squared form $X ^2 = \sum \left[ (Obs - Exp)^2 / Exp \right] $ can be computed, but these are far from large samples so its distribution under the null hypothesis will only be poorly approximated by the standard $\chi ^ 2$ distribution on 8 df. Instead, in keeping with other tests of this manual, the null distribution is simply created by permutation: 16 and 2 individuals are randomly and independently placed into the first and second set of replicates, respectively, and $X ^ 2$ recalculated many times. For T. discipes the observed $X ^ 2$ is larger than any number of simulated ones and $D=1$ can be firmly rejected, so the divisor of 3.1 is used, but for the final 6 species $D=1$ is not rejected (at p=5% on this one-tailed test), and no down-weighting is carried out.

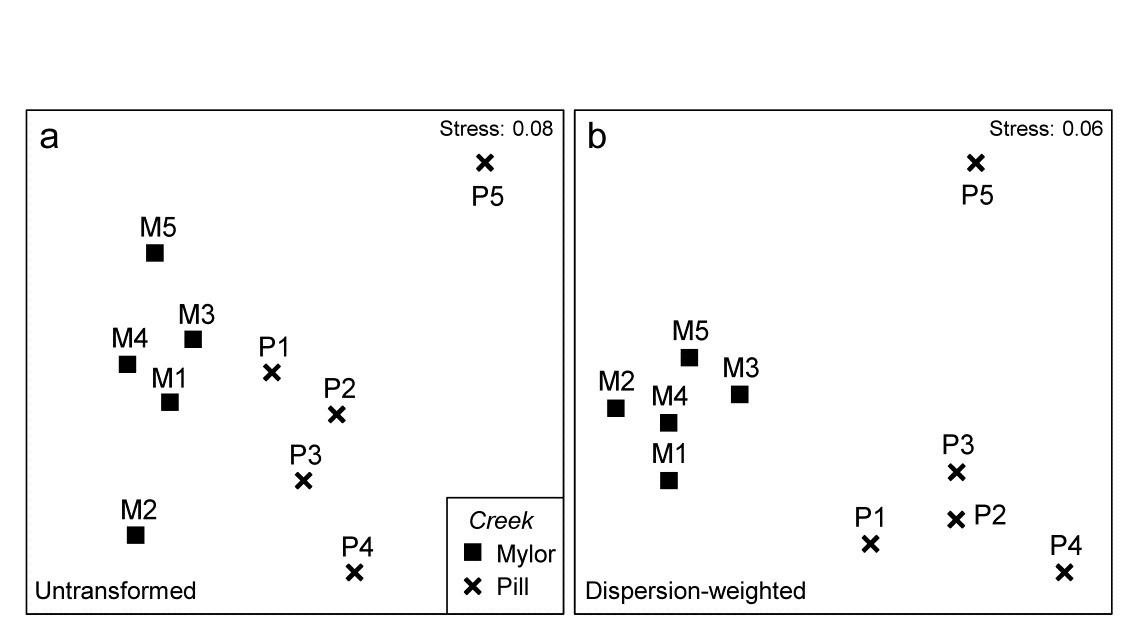
Fig 9.4 Fal estuary copepods {f}. MDS of copepod assemblages for 5 meiofaunal cores in each of two creeks (Mylor and Pill), from Bray-Curtis similarities on: a) untransformed counts; b) dispersion-weighted counts
 

Effect of dispersion weighting

The effect of DW on the multivariate analysis can be seen in Fig. 9.4, which contrasts the (non-metric) MDS plots from Bray-Curtis similarities based on untransformed and dispersion-weighted counts. A major difference is not observed, but there is a clear suggestion that the replicates within the M group in particular have tightened up, and the distinction between the two groups enhanced. The former is exactly what might be expected: by down-weighting species with large but erratic abundances in replicates we should be reducing the ‘noise’, allowing any ‘signal’ that may be there to be seen more clearly. But the latter cannot, and should not, be guaranteed. It is perfectly possible that when attention is focussed on the species that are consistent in replicates, they may display no change at all across groups – so be it. In fact, in this case, DW makes a sizeable difference to the ANOSIM test for the group effect, with the R statistic increasing from 0.41 to 0.71 after DW.
 

Shade plots to demonstrate matrix changes

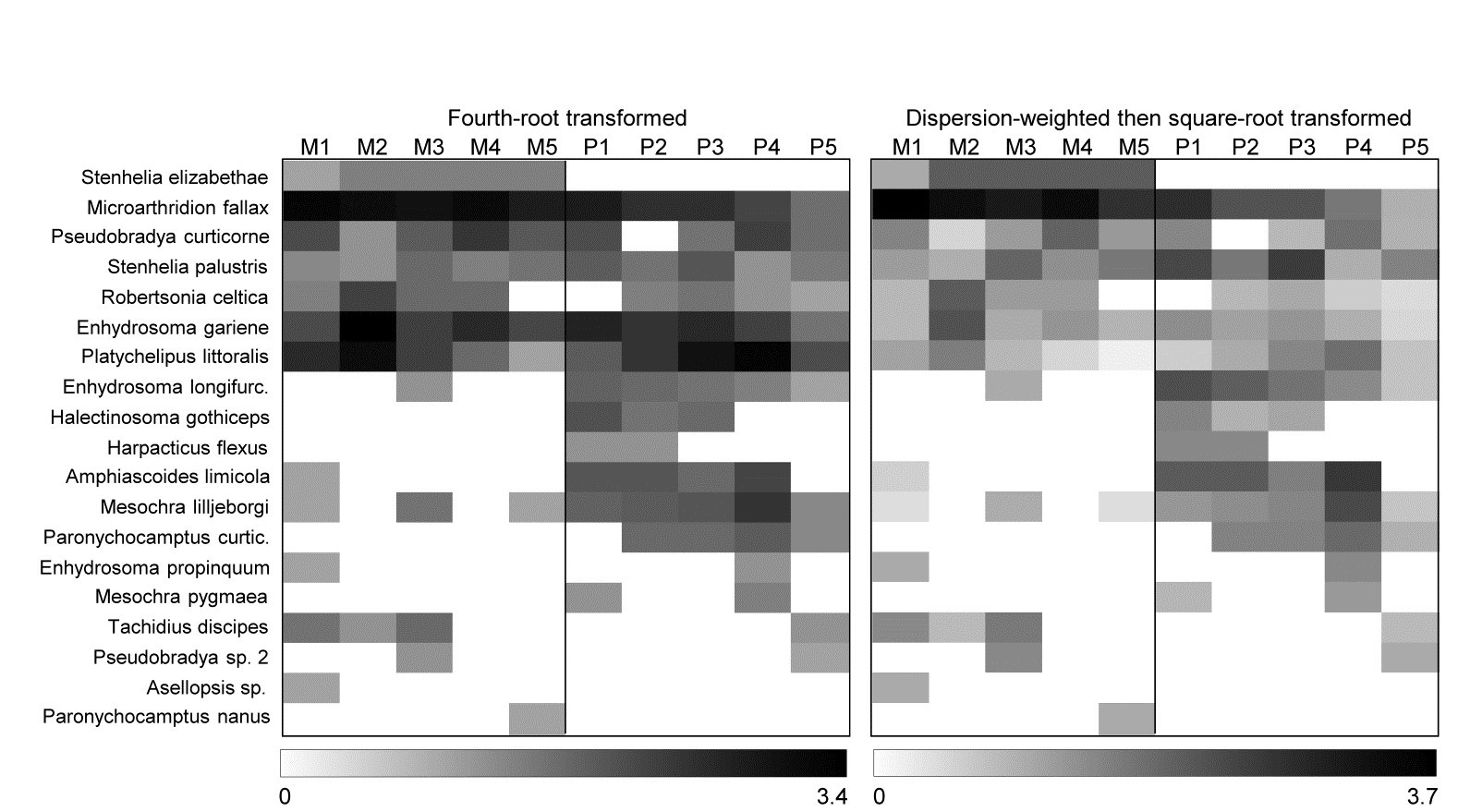
The explanation, in terms of particular species, for changes seen in the multivariate analyses following DW, are well illustrated by simple shade plots (p7-7, Clarke, Tweedley & Valesini (2014) ). For these visual representations of the data matrices, the intensity of grey shading is linearly proportional to the matrix entry, with white representing absence and full black the largest count (or weighted count) in the matrix, Fig. 9.5. Here, the species have been ordered according to a species clustering using the index of association on the original counts (equation 7.1), and the same species ordering is preserved for the shade plot under DW. It is readily seen that some of the less erratic species, such as M. fallax and S. elizabethae, do show a clear pattern of larger values at Mylor than Pill, and several other species which are not heavily down-weighted (Enhydrosoma longifurcatum, Amphiascoides limicola, Mesochra lilljeborgi) show the reverse pattern. The highly erratic species formerly given the most weight, P. littoralis and E. gariene, did not clearly distinguish the two creeks, so that their reduction in importance under DW has again, in this case, aided discrimination of the two groups.
 

Further DW issues

The DW procedure makes few assumptions about the data, but is derived from a model in which the degree of clumping, and thus the index of dispersion, of a particular species is constant across groups. In some cases this may well be a poor assumption, e.g. when impacts represented by a group structure affect both the propensity for that species to clump as well as the density of clump centres. Clearly, in that case, we must not use a different dispersion divisor D for each group; as earlier emphasised, doing different things for each group risks creating an artefactual group effect where none exists. Using an averaged index ($\overline{D}$) across groups might thus still provide a sensible ‘middle course’ in deciding how much weight to give to that species. Faced with the alternatives of doing no species weighting (so that erratic, clumped species dominate) or giving all species, abundant and rare, exactly the same weight (e.g. as in normalising the variables or the implicit standardisations of a Gower resemblance measure), DW may indeed be a robust general means of weighting species. As is seen later (e.g. Chapter 10 and 16 and Fig. 13.8), even quite major changes to the balance of information utilised from different species can have surprisingly little effect on a multivariate analysis, mainly because the latter typically uses only a small amount of information from each species and the same driving patterns are present in many species.

Fig. 9.5 Fal estuary copepods {f}. Shade plot, showing: left-hand, the untransformed counts of Table 9.6, represented by rectangles of linearly increasing grey scale (species clustering gives y-axis ordering); right-hand, the dispersion weighted values (maximum 13.4).
 

Clarke, Chapman, Somerfield et al. (2006) discuss further DW questions naturally arising. For example, should one upweight species that are significantly underdispersed, i.e. are territorially spaced, more evenly than expected under randomness, so that replicate counts are ‘too similar’ and chi-squared is significantly small? This is rarely observed, in the marine environment at least! Indeed, one of the beneficial side effects of applying DW is likely to be a clearer understanding of how a range of species are distributed in the environment, through histograms of dispersion indices calculated from all species in assemblages of different faunal types.

Also, how much more general can the DW idea be made? Clearly the test for D=1 is based on a realistic probability model for genuine counts but, if the testing structure is ignored, it would still logically make sense to apply downweighting by the variance-to-mean ratio for densities as well as counts, at least provided the adjustment from count to density was only of a modestly varying constant across samples. (A typical context might be where real counts from trawl samples are variably adjusted for modest differences in the volume of water filtered.) An extension to area cover data for rocky-shore or coral reef studies seems equally plausible. Here, the ‘counts’ can be thought of as number of grid points within a sampled area (one replicate) which fall on a particular species. If an individual algal or coral colony is larger than the grain of the grid points then the same colony will be ‘captured’ by several points, expressed as over-dispersion of the ‘counts’ from replicate to replicate (in the extreme, one species with an average area cover of 50% might vary from 100% in one replicate to 0% in the next, where another ubiquitous species, whose clump size is much smaller than the sampling grain, might record variation of only 40% to 60%). Relative down-weighting by dispersion indices then makes reasonable sense, and similar arguments could be adduced for biomass data of motile species. Larger-bodied species give greater ‘overdispersed’ biomass relative to smaller-bodied ones. In fact, by overlaying the previous model of real counts of organisms with a fixed body mass per individual (varying between species), relative downweighting by D works in exactly the same way as earlier, removing at the same time both greater clumping of individuals and the size differential between species, to leave a natural and robust weighting of the different species in subsequent multivariate analyses. It is, however, only relative D values that matter in all these cases; D=1 has no meaning outside the case of real counts.
 

DW vs. Transformation

DW is advocated above as an alternative to transformation, providing a more targeted way of dealing with large and highly variable counts in some species. The disadvantage of simple, severe transformations in this context (e.g. fourth root) is that, whilst effective in reducing the contribution of the erratic P. littoralis and E. gariene in the earlier example, they will also ‘squash’ consistent but low-abundance species, such as S. elizabethae, into a near presence/absence state. Nonetheless, simple transformations can be applied universally (e.g. without the need for replicates), and will often give similar results to DW. A fourth root transformation here actually leads to an even higher R value for the ANOSIM test for a group difference of 0.81, and the MDS plot, while similar, tightens up the Pill group by giving less emphasis to the lower total abundance at P5 than the other Pill creek sites; the latter was clearly seen in the shade plot, Fig. 9.5.

A shade plot for this fourth-root transformed matrix is shown in Fig. 9.6 (left-hand plot) and it is clear that the multivariate analyses will now mainly be driven by the differing presence/absence structure, with the originally important species playing a much smaller role (e.g. M. fallax now appears scarcely to differ between the two creeks).
 

DW and Transformation

However, the key step here is to realise that DW and transformation are not necessarily alternatives; it may be optimal to use them in combination. DW directly addresses the problem of undue emphasis being given to high abundance-high variance species, ensuring all weighted species values now have strictly comparable reliability. But DW does not address the primary motivation for transformations outlined in Chapter 2, that of better balancing the contributions from less abundant (and consistent) species with the more abundant (and now equally consistent) species. Not all high abundance species are erratic in replicates and, if they are, they may still have largely dominant values after DW has ensured their consistency. In short: DW is applied for statistical reasons but we may still need to transform further (after DW) for biological reasons, if we seek a ‘deeper rather than shallower’ view of the assemblage. That transform will likely now be less severe than if no DW had been carried out since it is no longer trying to address two issues at once. Here, the shade plot for DW followed by square root transformation is shown in Fig. 9.6 (right-hand plot) and this combination does actually give (marginally) the best separation of Mylor and Pill creeks in the multivariate analysis, amongst the analyses shown here, with R = 0.85.

Fig. 9.6 Fal estuary copepods {f}. Shade plot, with linear grey scale for: left-hand, 4th-root transformed counts; right-hand, dispersion weighted values subsequently square-root transformed. Species order kept the same as in (untransformed) species clustering, Fig. 9.5.
 

This is not an uncommon finding. Clarke, Tweedley & Valesini (2014) describe the role of shade plots in assisting long-term choice of better transformation and/or DW strategies, and give examples. One is of fish studies in which highly schooling species, though heavily down-weighted by DW (by two orders of magnitude), remain dominant because they are consistently found in some quantity in all replicates. DW followed by mild transformation was transparently a better option than either DW or severe transformation on its own.

‘Long-term choice’ is an important phrase here: one must avoid the selection bias inherent in chasing the best combination of DW and transformation for each new study – ‘best’ in the sense of appealing most to our preconceptions of what the analysis should have demonstrated! Instead, the idea is to settle on a pre-treatment strategy to be used consistently in future for that faunal type in those sampling contexts.