2-way crossed ordered test
The test for an ordered factor (A) in the 2-way crossed design parallels the construction seen earlier for the 2-way (unordered) crossed case, in that the 1-way R$^\text{O}$ statistic is calculated separately for each level of the other factor (B) and those R$^\text{O}$ values averaged to give the 2-way test statistic. This is compared with its null distribution calculated under the same constrained permutation procedure as for the previous 2-way crossed case – A labels are permuted only within the levels of B. The difference here, again, is that this is a perfectly viable test when there is no replication within the cells of the 2-way layout, provided there are enough ordered steps ($a$) in factor A or levels ($b$) of factor B to generate sufficient permutations, $ (a!/2)^b$, for a sensible test. This number scales up very rapidly, so even a fairly minimal design will give some sort of test, e.g. $a=4$ transect sites sampled $b=2$ times gives 144 permutations and (at best) a p<1% level test for the presence of site ordering. The 1-way test ($b=1$) requires at least $a=5$ ordered steps, to give 60 permutations for a p<2% test.
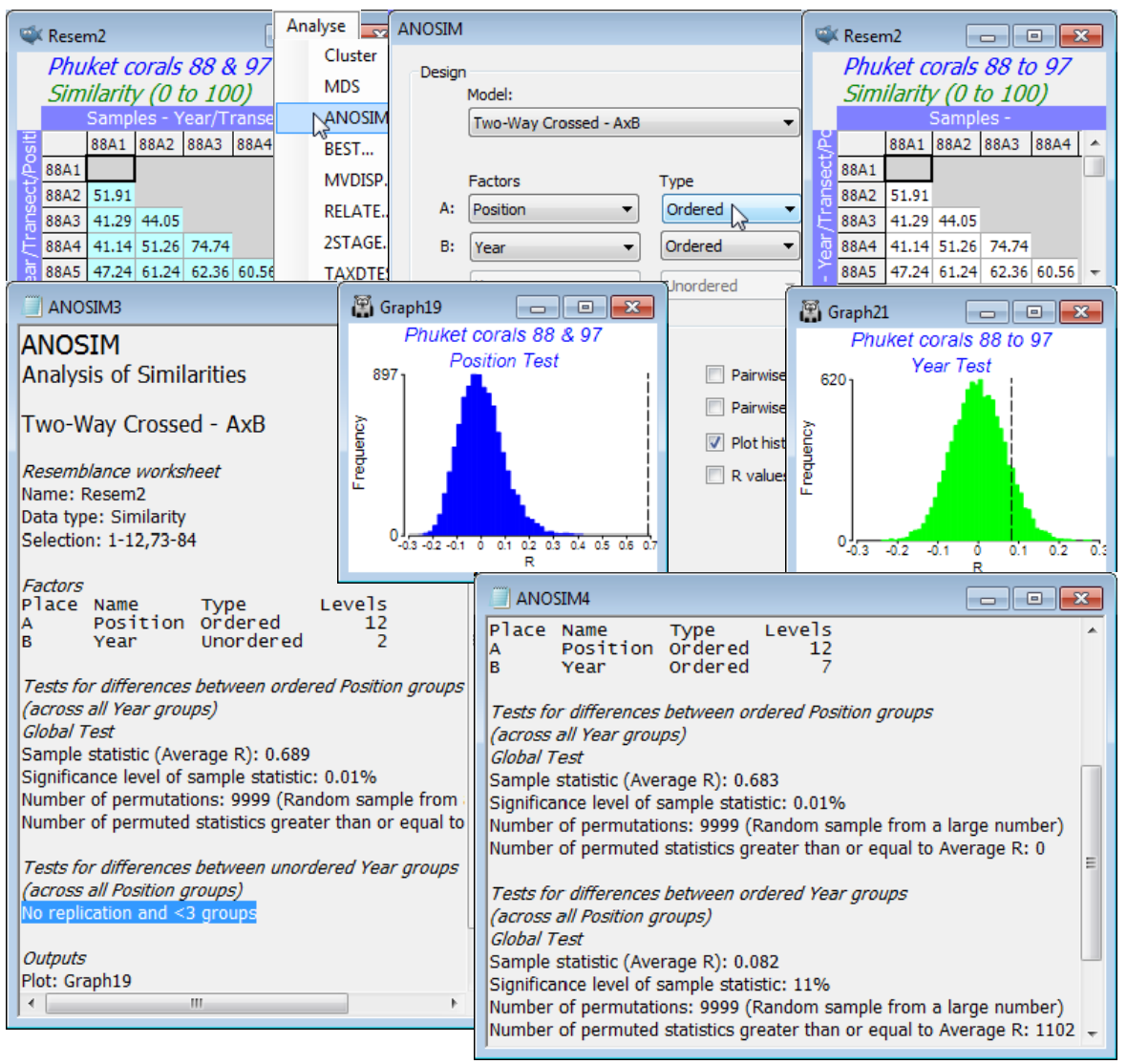
Run Analyse>ANOSIM>(Model•Two-Way Crossed - AxB)>(Factors A: Position Ordered & B: Year Unordered) on same resemblance selection as above, of the two years 88 and 97, together. This will, of course, produce a massively significant Position effect, with average R$^\text{O}$ = 0.69, and with (Max permutations: 9999) this is still off the top of the null distribution, p<0.01% (or, as a probability, P<0.0001). It is naturally a very powerful test, with $6 \times 10^{16}$ possible permutations.
It did not matter in this case whether the Year factor was defined as Unordered or Ordered, since there were only two years. The test for Year, removing the effect of Position by comparing years only within each of the 12 levels for Position, is doomed to failure, unsurprisingly. There are no replicates on which to base such a test (applying the above formula for an ordered test, a=2 so a!/2 = 1 and, whilst b=12 is large, powering up 1 still gives 1, i.e. there is only one permutation which is the observed configuration of the labels!). ANOSIM simply says No replication and <3 groups.
However, if we were to take off the selection, so reintroduce the full set of 7 years, and specify that both factors are ordered then there are ample steps in both the spatial gradient of 12 points and a temporal time trend of 7 points for an ordered test of either factor, removing the effect of the other. The Position test now gives a very similar R$^\text{O}$ = 0.69 as found for the two years alone but the Year test returns R$^\text{O}$ = 0.08, with about 1100 of the 9999 permutations created under the null hypothesis giving larger R$^\text{O}$ values than this (p<11%), a non-significant result. (Incidentally, note it is always true that a test of factor A is completely unchanged by whether factor B is assumed ordered or not).
In fact, whilst the original study postulated serial change in coral communities along the onshore-offshore transect, so that an ordered test for the Position factor seems very appropriate, it is not so clear that it is relevant to test for a monotonic inter-annual trend – a drift of the community in time, ever further away from its original configuration. Local impacts in some years may be dominant, and the possibility that these have a differential effect on the transect gradient (an interaction of a type) suggests a very different approach, using the Analyse>2STAGE routine, which we shall return to for these data in Section 14. Within the ANOSIM routines however, the 2-way crossed layout for an unordered factor with no replication leaves few options for a non-parametric test, though sometimes helpful is a fall-back test (available in PRIMER since the early versions), which is next described for the Exe estuary nematode data. Save and close workspace Phuket ws.