Transform on resemblances; Combining resemblances
Transforming resemblances remains in the Tools menu in PRIMER 7, since it is not an option for pre-treatment of data matrices prior to resemblance calculation (which characterises the other items on the Pre-treatment menu). Although not commonly required, it facilitates at least a couple of interesting analysis concepts. One is really outside the scope of this manual, namely to examine the extent to which the semi-parametric PERMANOVA tests are robust to (monotonic) transformation of the resemblance values, transformations which would not change the ANOSIM test results in any way (since they are based only on the ranks of the resemblances). It is empirically well-known, for example, that the square root of Bray-Curtis (unlike Bray-Curtis itself) does not give negative eigenvalues for the high-d PCO ordination which underpins the approaches in PERMANOVA+. Whether the consequentially poorer low-d PCO representation is a price worth paying for a PCO space without imaginary axes must be open to question, however. Tools>Transform on a single resemblance matrix provides a basic tool to assist in following up such questions. More simply, we have already seen it used (under Correlation as similarity in Section 5) to turn a correlation with values in ( 1, 1) into a similarity over (0, 100) by use of the transform Expression: 100*Abs(V).
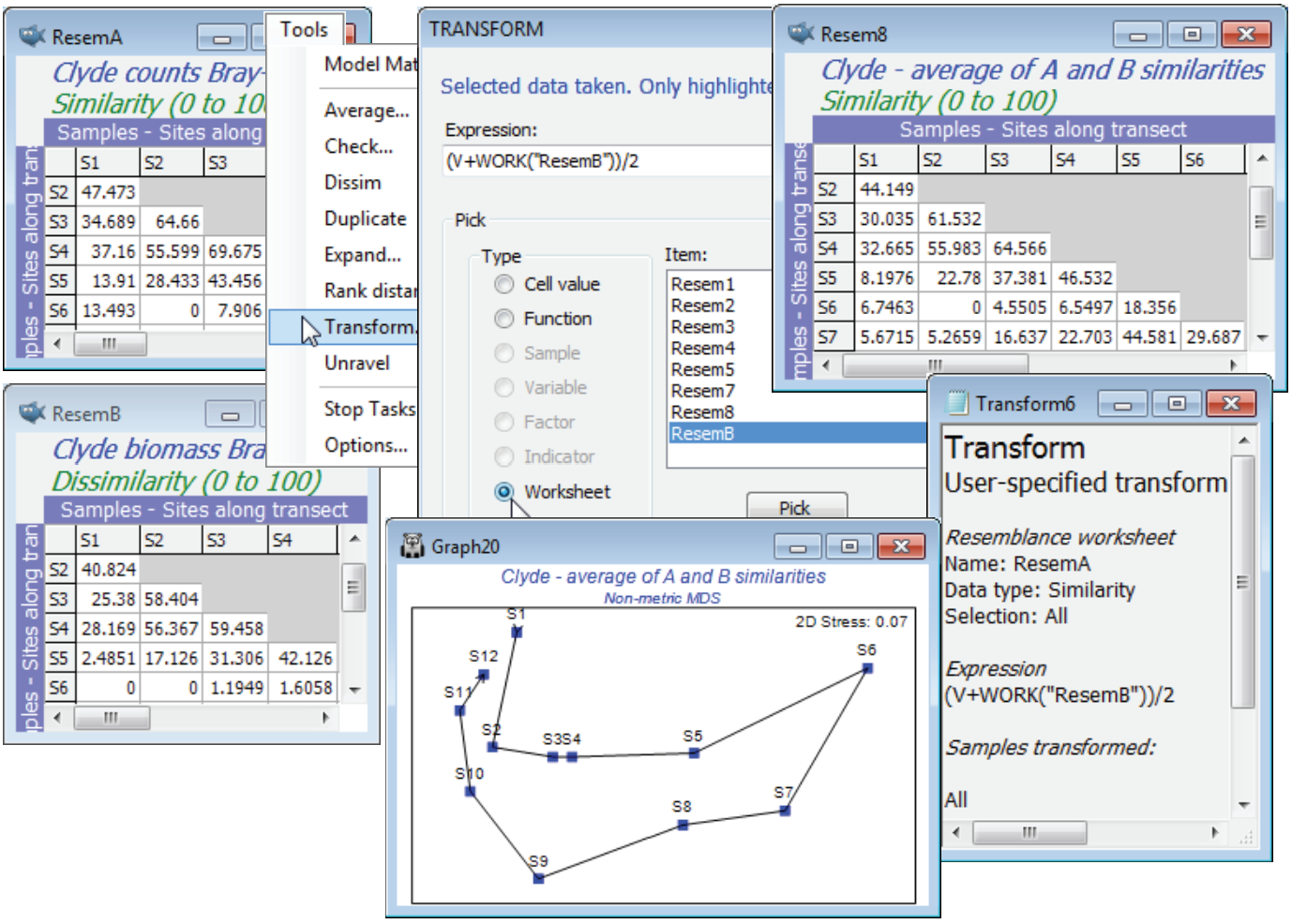
Another use of Tools>Transform on resemblance matrices is also less esoteric and potentially of substantial practical benefit. It provides an interesting solution to the handling of ecological data matrices from mixed faunal types, e.g. counts of motile organisms and cover of colonial species within the same rocky-shore quadrats. This type of problem was raised earlier (end of Section 8), when two resemblance matrices over the same set of samples were combined in a single MDS, by minimising an average stress function. The difficulty with that approach is that it only generates an MDS, and many of the methods in PRIMER do not work in the approximate low-d space of an ordination but on the full resemblance matrix (or usually its ranks). However, whilst counts and area covers are difficult to scale in relation to each other in a single data matrix, it is not difficult to calculate Bray-Curtis similarities (say) for a count matrix and a cover matrix separately, for the same set of samples, and then simply average the two resemblance matrices over every matching pair of entries using Tools>Transform, using a similar worksheet-based transform expression to that previously demonstrated. (Dis)similarity values in the range (0, 100) for both matrices will stay in (0, 100) under the arithmetic averaging expression of (A+B)/2 (or a weighted form, (3*A+B)/4, if the contribution of counts is considered roughly three times as important as that from area cover). Geometric averaging of the type seen above is also possible, e.g. (A*B)^0.5 or (A^0.75)*(B^0.25). If the two resemblance matrices are not on a common scale and direct averaging is not appropriate, a simple solution would be to run both through Tools>Rank distance, putting them on a common scale – and fitting well with PRIMER’s non-parametric approach – then averaging as above and re-ranking (though the latter is unnecessary for most PRIMER routines, which do their own ranking).
A simple example using two resemblance matrices can be constructed with the Clyde data, namely the Bray-Curtis site similarities averaged over abundance and biomass measures. So, instead of combining the data matrices (as in the earlier $A^{0.25} B^{0.75}$), we average the A and B resemblances. There is likely already to be a Bray-Curtis similarity matrix based on the square-root transformed biomass data from Clyde macrofauna biomass in the workspace (rename it ResemB) and you should now also compute Bray-Curtis similarities from Clyde macrofauna counts, this time on fourth-root transformed data (there is no reason why a different transform should not be appropriate for abundance than for biomass data). Then with the abundance similarities ResemA as the active sheet, take Tools>Transform>(Expression: (V+Work(“ResemB”))/2), change the title of the result appropriately, and run Analyse>MDS to compare this with the earlier (ranked) biomass MDS.