Global BEST test

The question of statistical significance testing on the results of the Bio-Env (or BVStep) procedure naturally arises. Section 14 describes Analyse>RELATE, a (non-parametric) form of Mantel test. For any two independently-derived resemblance matrices, defining the relationships among the same set of sample labels, one can use permutations to test the null hypothesis H$_0$: no agreement in multivariate pattern. The measure of agreement is the (usually rank) correlation coefficient $\rho$, discussed above, between the corresponding elements of the two triangular arrays, with $\rho$ = 0 representing the null hypothesis. The $\rho$ values that it is possible to observe by chance, if the null hypothesis is really true, can be generated by randomly permuting one set of sample labels relative to the other (thus destroying any real link) and recalculating $\rho$, over many random permutations. RELATE could therefore be applied to testing agreement between an assemblage and the full set of environmental variables for the same sites (though not for all other linkage problems mentioned earlier, e.g. between the full assemblage and a subset of conspicuous species, since independence is violated – any subset of species will bear some relation to the full set). It is important to realise, however, that RELATE cannot be applied to the subset of environmental variables that result from a run of BIOENV: these have been selected precisely to maximise the matching coefficient $\rho$ with the assemblages. Even where there is no real match, the optimum $\rho$ produced by BIOENV will inevitably be >0. We need a test which allows for this selection bias, and this is the global BEST test (Clarke KR et al 2008, J Exp Mar Biol Ecol 366: 56-69, and Chapter 11, CiMC), a permutation procedure accessed on the first dialog box from Analyse>BEST. The idea is simple: randomly permute one set of sample labels in relation to the other, then run through the full BIOENV (or BVSTEP) process to generate the best match $\rho$. Another permutation of the labels is then generated and the BIOENV run repeated again, and so on (for 99 times by default, because of the intensive computation involved – but preferably more). This produces 99 values of $\rho$ in a histogram, which represents the null hypothesis. The real $\rho$ is compared with these, as for any PRIMER permutation test – if it is larger than any of them, then the null hypothesis can be rejected at p<1% significance. Actually, this is the sole example in PRIMER of a statistic ($\rho$) which does not take the value 0 for the null hypothesis – as indicated above, the mean $\rho$ is certain to be >0 under H$_0$.

When the new 2-way BEST routine is run, by taking the option (described earlier) to remove the effect of a categorical variable by matching only within its levels, the test proceeds in the same way but with a constrained permutation of biotic sample labels within – not across – those levels.

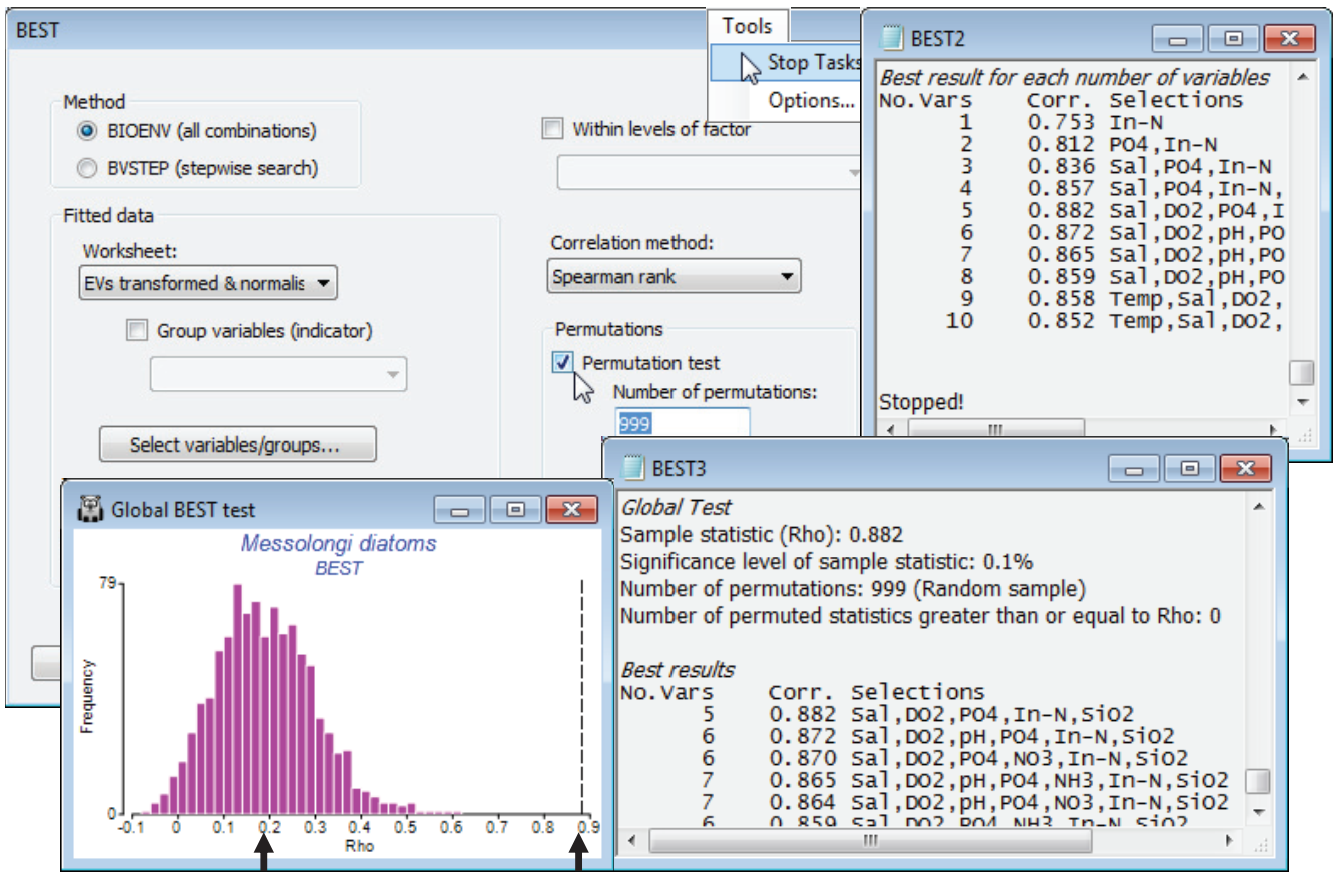
From an active sheet of the lagoon diatom resemblance matrix, re-run Analyse>BEST>(Method• BIOENV) & (Worksheet: EVs transformed & normalised) with most options as before but this time taking (Permutations✓Permutation test)>(Number of permutations: 999) & (✓Plot histogram), and (Variable naming•Full names). On a slow machine, or with more samples than here, you will probably need to reduce the number of permutations to 499, or 199, or 99. The latter is adequate if the result is clear cut, but results in a much less smoothed histogram, and you will wish to calculate more in border¬line cases. Remember that you can use always use Tools>Stop Tasks (or the icon on the Tool Bar ) to interrupt a permutation test that, from observing the green progress bar, is clearly going to take too long – note that since it computes and outputs the BEST results tables for the real data before embarking on the random permutations, you will not lose these if you stop the routine prematurely. An alternative is to multi-task, carrying on with other PRIMER activities as the permutation test runs in the background – this is not a problem. In addition to generating a null distribution histogram (for which you can change the bin size, colours etc with Graph>Special as usual), the test adds a small section to the results window, headed Global Test, whose format is as for the ANOSIM test, Section 9. It gives the real value of $\rho$ and its % significance, 100$\times$(1+(no. of permuted $\rho \ge$ observed $\rho$))/(1+no. of perms). The real $\rho$ (0.88) is well to the right of the upper tail of the null distribution, p<0.1% (i.e. P<0.001). Note also that the mean of the histogram is not zero but around $\rho$ = 0.2. The strong selection pressure, over a large number of variable combinations, is able to produce an artefactual match up to about $\rho$ = 0.4 or even 0.5, though there is no question that the null hypothesis is rejected here – such a good match of water column indices to the diatom assemblages, as seen in the earlier biotic and abiotic MDS plots, clearly cannot be due to chance. A final step would be to select only the BEST set of abiotic variables and repeat the Euclidean MDS.