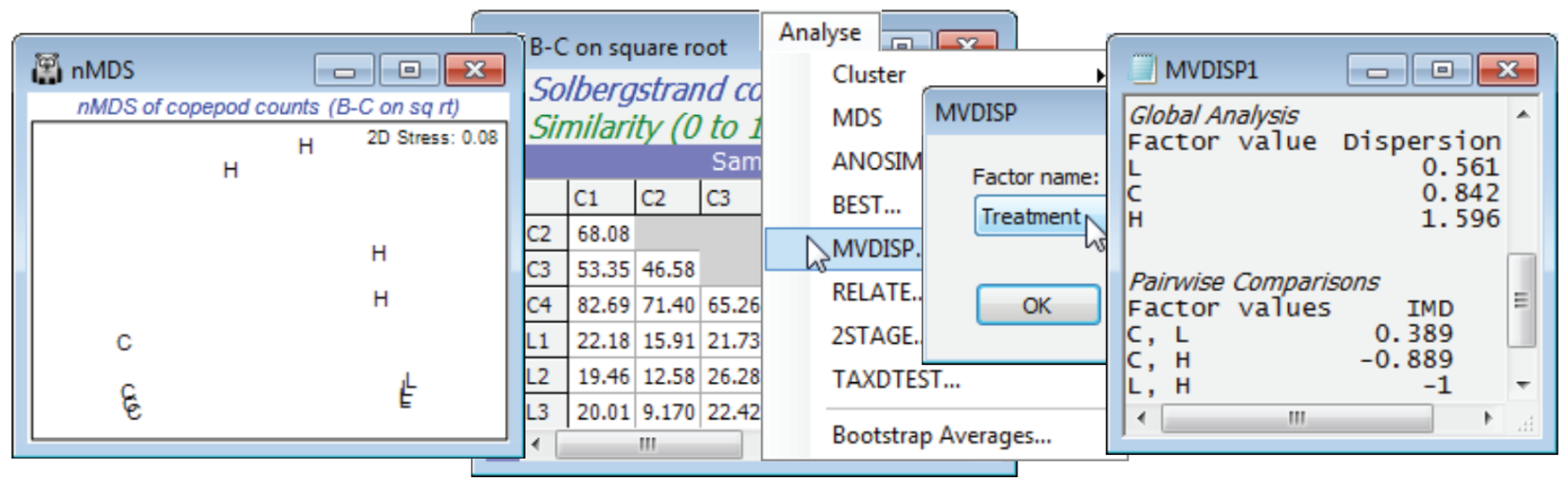
(Mesocosm experiment, Solberg¬strand copepods)
The illustration used here is a simple 1-way design of 3 mesocosm treatments: Control (C), Low (L) and High (H) dose of organic enrichment applied to the surface of 12 intact sediment cores, taken from the same location into a mesocosm system, and randomly allocated to the treatments (with 4 replicates in each). Data are from Gee JM et al 1985 J Exp Mar Biol Ecol 91: 247-262, as analysed in a multivariate way by Warwick RM & Clarke KR 1993 “Increased variability as a symptom of stress in marine communities” J Exp Mar Biol Ecol 172: 215-226. Chapter 15, CiMC shows analysis of the resulting meiofaunal communities in the sediment cores (nematodes and copepods) after several weeks’ exposure, but here we open just the copepod data, Solbergstrand copepod counts in C:\Examples v7\Solberg copepods. For square-root transformed data and Bray-Curtis similarities, plot the nMDS and note the apparently much larger dispersion within the High dose treatment (as well as the obvious differences between treatments, which would be tested, validly, by 1-way ANOSIM). This is indicated more reliably, i.e. not in the low-d approximation of an ordination plot, by running Analyse>MVDISP>(Factor name: Treatment) on the resemblance matrix. The dispersion sequence of 0.56, 0.84, 1.60 for L, C, H shows that the average rank dis-similarity is almost three times higher within H than L (comparable dispersions result in a sequence of 1’s), and the pairwise comparisons show that all the lowest dissimilarities (within a group) are in L and all the highest in H (thus IMD = –1 for that pair of treatments). The result, however, is of limited useful¬ness since an exact permutation test of these dispersion differences is not possible under the non-parametric framework in PRIMER, for much the same reason as interaction tests in a two-way crossed layout are not possible, see the comments at the end of Section 9 and Chapter 6 of CiMC. [No permutation procedure exists under a null hypothesis that the dispersions are the same for each group, but that the ‘locations’ – in so far as they are defined for rank-based dissimilarities – may differ. If the primary interest is in testing for differences in multivariate dispersion of groups, for a given resem¬blance measure, you should use the (approximate, semi-parametric) permutation test given by the PERMDISP routine in PERMANOVA+ – see the Anderson et al 2008 manual. The parameters defining centroids of each group in the high-d PCO space are estimated and each centroid is moved to the same point, justifying permutation of the samples across groups under the null hypothesis – if location differences have been removed, and the null hypothesis specifies no dispersion differences, then sample labels again become interchangeable.]