Corrections for missing data
Returning to the main purpose of resemblance measures, to describe similarity among samples, an important new feature in PRIMER 7, not offered in earlier versions, is that resemblance measures will now be calculated in the presence of missing cells (identified by Missing! in the sheet). As described in Section 1 (box heading Missing or zero values?) this tends to arise only for sheets of type Environmental or Other – species matrices can have whole samples missing from an otherwise balanced layout but this is not regarded as missing data, just unbalanced design, handled routinely in PRIMER (and PERMANOVA+). Under restrictive conditions (multivariate normality in a ‘not too high’ dimensional space) it may be possible for some environmental data to estimate single entries missing at random, utilising the correlations between variables (see Tools>Missing in Section 12) but in many contexts for which missing entries are almost guaranteed, these modelling conditions will not apply. An example would be would be questionnaire data, in which the samples are the individual respondents and the variables the questions, e.g. with matrix entries 1 to 5, for a ‘disagree strongly’ to ‘agree strongly’ scale. This is a likely area for application of multivariate methods, calculating similarities between respondents in the profile of answers, and linking this to demographic/socio-economic data, e.g. PRIMER applications from environmental economics exist, but missing answers are commonplace and probably not estimable under normality assumptions.
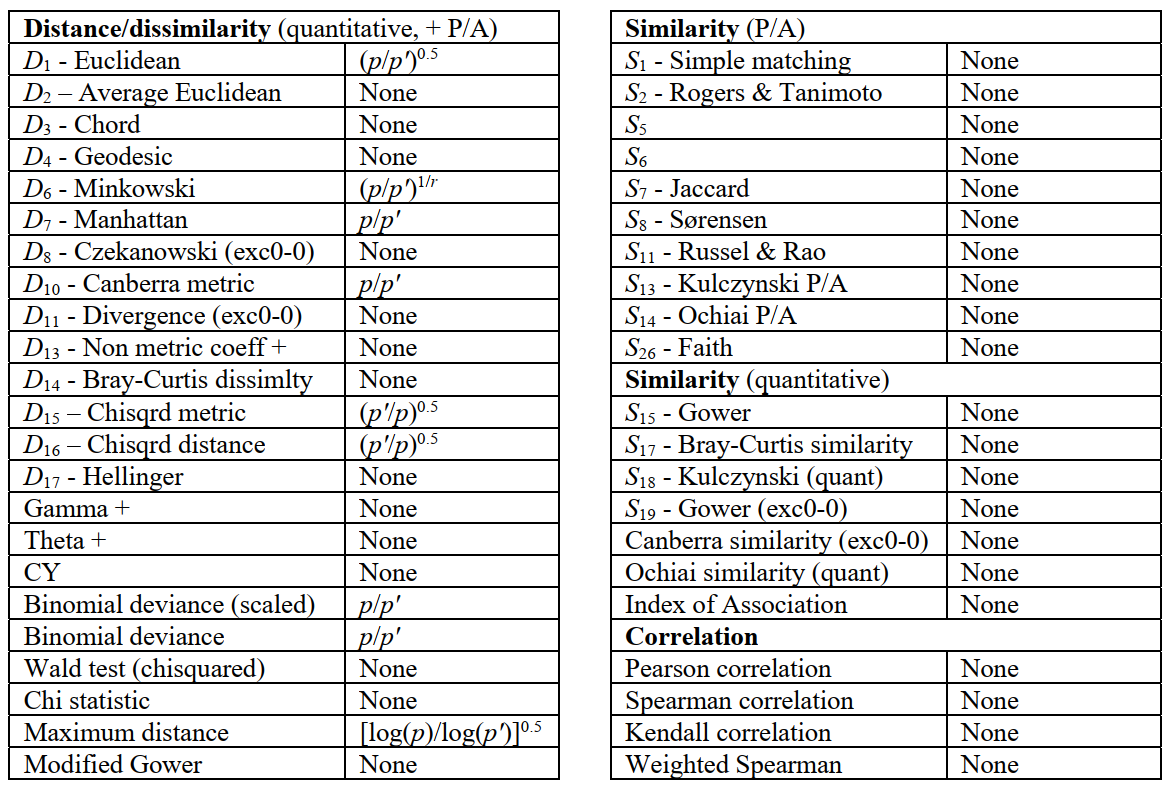
Where there is missing data, PRIMER 7 therefore computes a resemblance between each specific pair of samples by removing (for that calculation only) those variables in which one or other value is missing (referred to as pairwise elimination of missing data). This can cause a crude bias in some distance measures which are in the form of sums rather than averages of variable contributions, in that pairs of samples with many missing entries will automatically return lower distances than those with few or no missing values, all else being equal. Examples are Euclidean ($D_1$) or Manhattan ($D_7$) distances, which are both based on simple sums over the variables. A correction for these biases is straightforward in this case: average Euclidean distance ($D_2$) clearly has no such crude bias since the contributions from each variable are averaged not summed. The solution for $D_1$ is therefore to multiply up the summation by a factor ($p/p^′$), where $p$ is the full number of variables in the array, and $p^′$ is the number of variables used in that specific sum, having pairwise-eliminated the missing variables. The outer square root in the definition of $D_1$ makes the overall correction term $(p/p^′)^{0.5}$.
PRIMER 7 automatically applies such correction factors to every resemblance measure, if needed, as shown in the following table. Note that the standardisation implicit in many measures, including all (dis)similarities, avoids the need for correction, sample totals always being re-defined for each pairwise-eliminated set. The corrections have only asymptotic justification for the more complex measures, e.g. $D_{16}$ Chisquared distance for which the correction term is $(p^′/p)^{0.5}$, not $(p/p^′)^{0.5}$, thus a downward adjustment. (Similarly, that for Maximum Distance is based on Jensen inequalities on asymptotics of extreme value distributions so is definitely approximate!). It should be stressed that these corrections assume an average contribution from each missing variable, as measured by the average for the present variables. Broadly, this is not unreasonable if values are missing at random, but is theoretically inferior to reconstruction of missing values by Tools>Missing, when the strict conditions for this apply, since that uses variable correlations to estimate non-average values.