2-way RELATE for seriation
A new feature in PRIMER 7 parallels that discussed for the BEST analysis of the previous section, namely a secondary factor is supplied, e.g. (✓Within levels of factor ), which turns this into a 2-way RELATE test. The matching statistic $\rho$ – whether that is to simple seriation, simple cyclicity or a supplied resemblance/model matrix – is calculated only on samples within the levels of this secondary factor, and the $\rho$ values averaged to give the overall test statistic. The permutations for the test are similarly constrained to be within the strata of this eliminated, secondary factor.
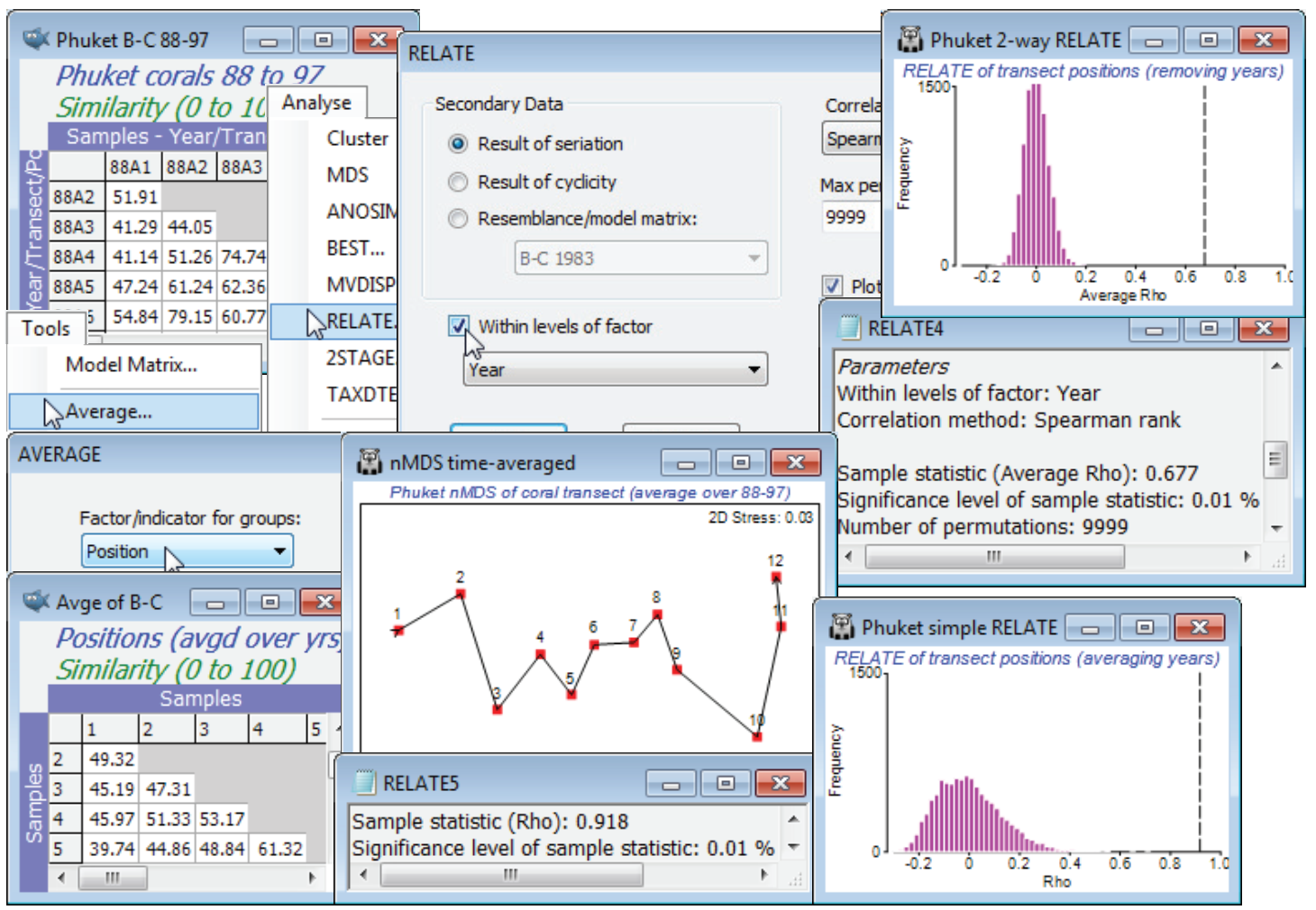
In the current Phuket ws workspace, open (if necessary) the data file Phuket coral cover 88-97, and run the same root-transform and similarity as above, for these 12 transect positions $\times$ 7 years – a period with no known new stressors on the coral reef. Running RELATE on this similarity matrix, under the simple (•Result of seriation) model, and for (Within levels of factor Year ), removes the inter-annual differences by calculating a simple trend statistic $\rho$ across the transect positions, separately for each year, and then averaging those. (Note again that since we have not supplied the Position factor in setting up the test, the routine presumes that the samples for each year are in the desired serial order in the matrix). This is now a test statistic for the null hypothesis of no serial community change along the transect in any year, giving a large average $\rho$ of 0.68, and obviously an overwhelmingly significant result (p<0.01%). An alternative test would have been to average the samples over the years for each transect position (by Tools>Average using factor Position, on either the transformed data or the similarity matrix) and perform a simple seriation test on the 12 samples of the resulting matrix. As the nMDS plot for these averages shows, there is a very steady time-averaged gradient of change along the transect with RELATE statistic $\rho$ = 0.92 (p<0.01%). However, the histogram of the null distribution is seen to take values up to 0.3 or 0.4, in contrast with that for the 2-way RELATE test for which values larger than about 0.1 will be significant. In other words, 2-way RELATE is the more powerful test – by eliminating the year differences rather than averaging over them it has many more permutations and this could be important for testing very short runs of serial change (an averaged test with 5 transect positions has only (5!/2) = 60 distinct permutations, at best an $\approx$2% level test, and 4 positions is not viable, with 12 permutations).
The above example was met in Section 9, under the 2-way ordered, unreplicated ANOSIM test, and there is again a very close affinity of the average $\rho$ statistic with the average ANOSIM R$^{\text Os}$. In fact, there is no advantage here in using the 2-way seriation RELATE test – the equivalent ordered ANOSIM test is marginally preferable (see Chapter 6 in CiMC on ANOSIM for ordered factors). However, ordered ANOSIM is constrained to the simple serial model, whereas 2-way RELATE comes into its own, later, when we move to other model matrices, e.g. seriation for a time series where the times are not equally spaced, and we wish to allow for this in computing the statistic (though in most cases that will make very little difference because of the rank nature of the tests) or, more importantly, when the model is not serial but cyclic, or based on a supplied resemblance matrix from abiotic variables, perhaps. This takes us back to the 2-way BEST construction of the previous section – matching to an environmental resemblance matrix, having removed a categorical factor. The difference of 2-way BEST from 2-way RELATE, of course, is that between any global BEST test and an equivalent RELATE test – the former allows for the selection bias in repeating abiotic variable choices until the best match is found, whereas the latter assumes a single fixed set.
Save the workspace Phuket ws, which will be returned to later in the context of 2nd stage analysis.