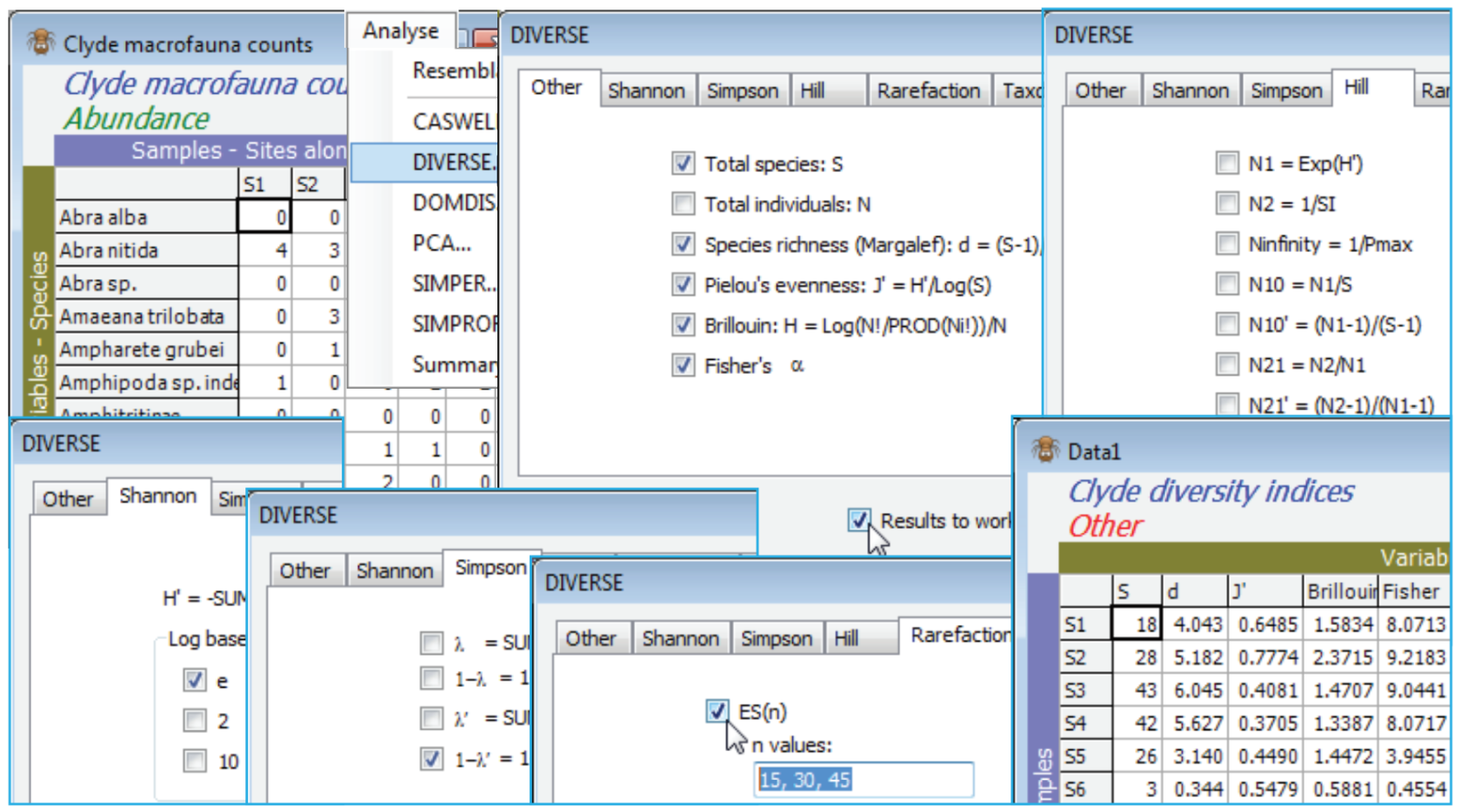
Standard indices calculated
The range of indices available is illustrated with the macrobenthic data Clyde macrofauna counts from the Clyde sludge dump-ground study, directory C:\Examples v7\Clyde macrofauna, last seen in Section 14. Analyses so far have used only the abiotic and biomass matrices, and the existing workspace Clyde ws may have become cluttered, so open Clyde macrofauna counts into a new workspace, and save it as Clyde ws2. Without pre-treatment, take Analyse>DIVERSE>(✓Results to worksheet). Look at the options on the first 5 tabs, taking only ✓S, ✓d, ✓J$^\prime$, ✓H, ✓$\alpha$, ✓H$^\prime$ (log base e), ✓1 – $\lambda^\prime$, ✓ES(n) with n values: 15, 30, 45 (there is no special significance to the index grouping under tabs, except that the last two tabs deal with taxonomic-relatedness measures, seen later). The abundance of the ith species is denoted by N$_i$ (i = 1, 2, .., S) and, as a ratio of their sum (N), this is denoted P$_i$ (i = 1, 2, .., S). The first 5 tabs (where ✓ denotes the default selections) are:
Other
✓Total species: $S$
✓Total individuals: $N$
✓Species richness (Margalef): $d = (S – 1)/\log_e N$
✓Pielou’s evenness: $J^\prime = H^\prime / \log_e S$
Brillouin: $H = N^{-1} \log_e \{ N! / (N_1!N_2!…N_S! ) \} $
Fisher’s $\alpha$ statistic
Shannon
✓$H^\prime = – \sum P_i \log(P_i)$, where the logs are to the base e
$H^\prime$ as above but for logs to the base 2
$H^\prime$ as above but for logs to the base 10
Simpson
$\lambda= \sum P_i^2$
$1 - \lambda= 1- (\sum P_i^2)$
$\lambda^\prime= \{ \sum_i N_i (N_i–1)\} / \{N(N–1) \}$
✓$1-\lambda^\prime= 1- \{ \sum_i N_i (N_i–1)\} / \{N(N–1) \}$
Hill numbers
$N1 = \exp (H^\prime)$
$N2 = 1/ \sum P_i^2$
$N_ \infty = 1/ \max_i \{P_i\}$
$N_{10} = N1/S$
${N_{10}}^\prime = (N1–1)/(S–1)$
$N_{21} = N2/N1$
${N_{21}}^\prime = (N2-1)/(N1-1)$
Rarefaction (Sanders/Hurlbert)
$ES_n$, the ‘expected’ number of species from $n$ individuals ($n \le N$)